变分法

是微分学中处理单变量函数极大极小部分的一种推广。变分法中的函数在实质上依赖于无穷多个独立变量，从古典的角度来看，这些函数通常都是一个积分，其被积函数依赖于一个函数，而不可能用有限多个参数来描述。例如，设R是m个变数x_1x2,…，x_m的空间中的一个光滑有界域，y是R上某光滑函数类中的任一函数，它在实数或几个实数组中取值，并且在边界上取给定的值。令f_(x,y,p)是2m+1个变量x₁,x₂，…，x_m,y,p₁,p₂，…，P_m的光滑函数，则积分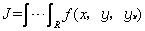

是从函数y的空间到实数域的一个函数，除非加上特殊的限制，这个函数是无穷维的，这里yx= ∂y/∂x
变分法研究这种函数及其极大极小，参加比较的函数的范围是现实地作出的，在足够的限制下，可以得到一个有价值的理论；在这些限制中不一定包含上述的固定边界条件。
目前，变分法在物理学等领域应用较为广泛，例如平衡位置或平衡轨线可以由能量或作用积分为极小予以决定。