反射法解作图题fanshefa jie zuotuti

也叫对称法，是利用一个图形关于一直线反射的方法作出所求的图形.
反射法常用来解决作等角、平分角问题、差角问题、倍角问题、垂直平分线问题和最小距离问题.
例如，如图，已知点A和⊙O在直线XY的同侧.在XY上求一点P，从P引⊙O的切线PB，使PA,PB与XY夹等角.
分析 设P点为所求的点，那么有∠1=∠2.假定固定直线XY，将图形翻折，使点A移到A′，那么∠1=∠3，因此，∠2=∠3.所以A′,P,B三点共线.由此可得作法.

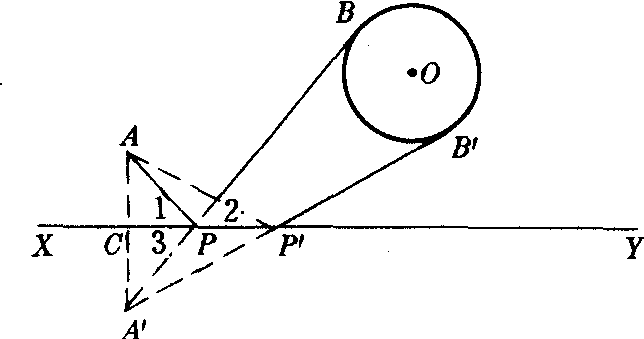
作法
❶过A作AC⊥XY于C，延长AC至A′，使CA′=AC.
❷过A′作⊙O的切线交XY于P，则P点就是所求的点.
证明 因为△ACP≌△A′CP，所以∠1=∠3.又因为∠2=∠3，所以∠1=∠2.
讨论 因为过A′所引⊙O的切线有两条，所以本题有两解.