双变量正态分布

当两个随机变量之间有直线相关关系，且这两个变量各自均服从正态分布，就形成双变量正态分布，它的图形称双变量正态曲面或正态相关曲面。
正态相关曲面的图形和方程 相关表（如下表）是X、Y两变量结合起来分组的复合表。在相关表上，若以各组段所形成的方格内的频数为Z，则双变量的频数分布呈立体形。当X和Y均为正态分布，X与Y之间是直线相关，样本含量越大，分组越细时，此分布将逐渐形成以X、Y、Z为坐标的正态相关曲面，如图1。其平行于X Y坐标平面的截面为椭圆形(如图2)，相关的程度越高，椭圆越扁。正态相关曲面的方程为

式中N为总例数，ρ为总体相关系数，μX和σX为X的总体均数和标准差，μY和σY为Y的总体均数和标准差。上述参数未知时，分别以样本的相应统计量来估计。

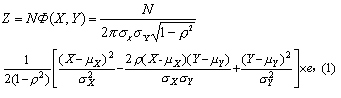
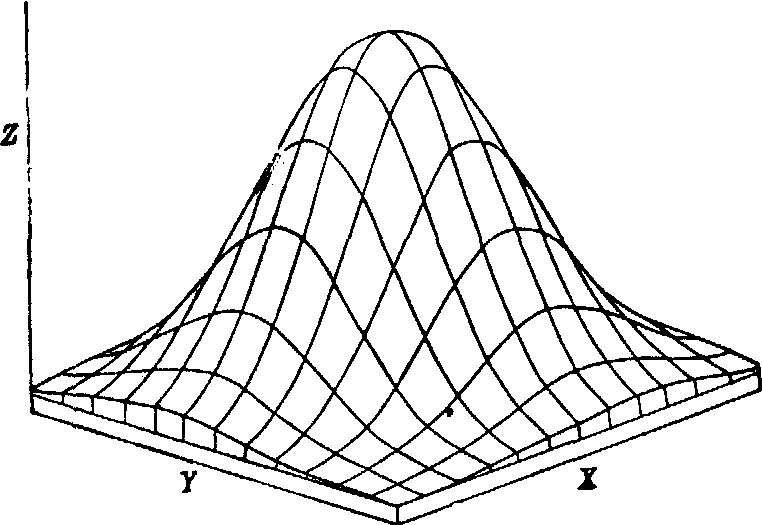
图1 正态相关曲面

正态相关曲面的三个重要特性是：
❶任何与XY坐标平面平行的水平截面均为椭圆形。ρ的绝对值越大，椭圆的短轴越短，当ρ→±1时，以其回归直线为极限；ρ的绝对值越小，椭圆的短轴越接近于其长轴，当ρ→0时，以圆为极限。
❷任何与ZY坐标平面平行的截面，其周边均为正态曲线，这些正态曲线的均数之轨迹就是由X推算Y的回归直线。
❸任何与ZX坐标平面平行的截面其周边亦为正态曲线，其均数之轨迹是由Y推算X的回归直线。
计算正态相关曲面时资料的适用条件是：
❶大样本计量资料；
❷X与Y两个变量之间必须有相关联系；
❸X、Y服从双变量正态分布或近似双变量正态分布，否则应先作变量变换使之正态化。
正态双变量资料的分析方法
(1)计算大样本相关系数和回归系数等。在相关表上用简捷式(2)～(4)计算离均差平方和及积和：

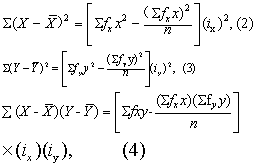
式中f_x和f_y分别为X变量和Y变量各组段的频数； f为相关表小方格内的频数；i_x和i_y分别为X变量和Y变量各组段的组距。

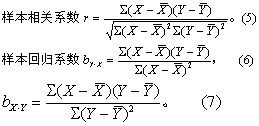
由X推算Y的回归线l_Y·X的方程为

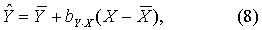
由Y推算X的回归线l_X·Y的方程为

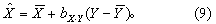
(2)将(X,Y)值作散点图，显示双变量资料的个体分布。
(3)按照双变量正态分布包括个体的百分数，可计算上述水平截面的椭圆在XY平面上的投影，用于估计在相关条件下的个体正常值范围。水平截面的椭圆方程

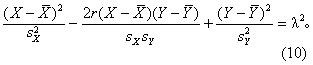
式中均以样本统计量作为相应总体参数的估计值。λ与概率水准α及r有如下关系：

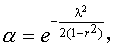
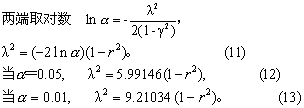
由式(10)与式(12)可作包含95%个体值在内的椭圆，由式(10)与式(13)可作包含99%个体值在内的椭圆。
例 某市156名10岁女童的身高(cm)和体重(kg)的频数分布经整理后如表。试计算相关系数，并作假设检验；求直线回归方程；计算椭圆方程；作图并分析。

某市10岁女童的身高体重相关表

(1)按相关表计算基本数据。
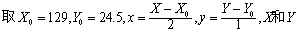为组中值。 计算fxx, _fxx², fyy ,fyy2，方法与单变量时相同。
计算∑fx，如横行内1(8)=8,横行内1(-4)
+3(-2)+12(-1)+3(0)+1(1)+2(2)=-17，余类推。注意，表下方倒数第二行∑fxx必须与表右起第二栏的∑fx总计相等，此例均为-72。再计算∑fxy，见表最右栏。
(2)计算相关系数并进行假设检验。
H₀:ρ=0,
H₁:ρ≠0。
α=0.05。

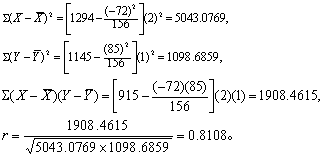
v=156-2=154，查相关系数界值表，得P<0.01，按α=0.05水准，拒绝H₀，接受H₁，故可认为X与Y有直线关系。(3)计算回归系数及回归方程，(参见条目“直线回归”)。

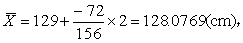
(4)计算正态相关曲面方程及其水平截面椭圆方程。
按式(1)计算正态相关曲面方程：

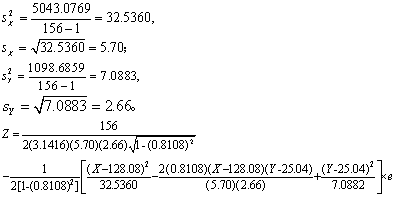
简化得：

按式(12)、(13)及式(10)求水平切面椭圆方程：
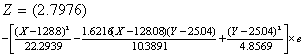
α=0.05 λ²＝5.99146[1-(0.8108)²]=2.0527,α=0.01 λ²＝9.21034[1-(0.8108)²]=3.1555,

(5) 作图。将156人身高、体重的原始数据画散点图(图2)；按lY·X的方程及lX·Y的方程作两回归直线；把适当的X值代入95%和99%范围的椭圆方程，即得相应的Y值，再以此各对数值(X,Y)作图，就是图2上的两个椭圆。内椭圆表示95%范围，实际包括149个点子，占149/156=95.5%:外椭圆表示99%范围，实际包括154个点子，占154/156=98.7%，均与理论估计很接近。作图时，注意椭圆在X方面的极大点和极小点就是它与直线lY·X相交的二个交点，在Y方面的极大点和极小点就是它与直线lX·Y相交的二个交点。计算极值点时，把椭圆方程与直线回归方程联解即得。
(6)分析。本例椭圆的短轴与长轴相差悬殊，表明身高与体重相关密切。图2中分布于右上方的点子代表身高与体重均达到同年龄、性别中的较高水平者；左下方的点子代表身高与体重均在较低水平者； 分布于邻近回归线的点子代表“匀称”的体型（无论水平高低），而右下方的少数点子属于“瘦高”体型，左上方的少数点子则属于“矮胖”体型。

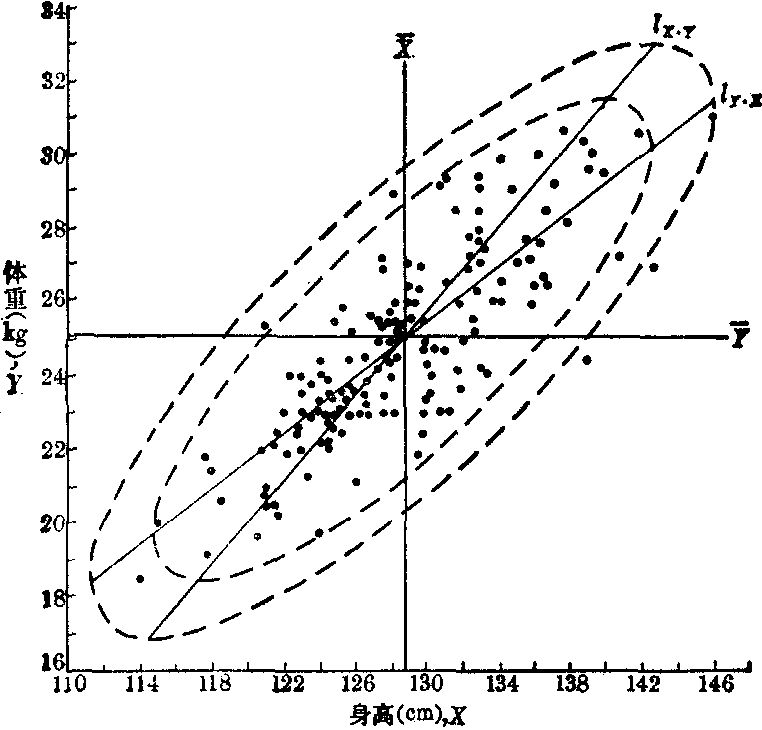
内圆：95%范围 外圆：99%范围
图2 10岁女童身高与体重相关图及其正常值范围