卡方分布chi-squared distribution
设x1、x2、…,xn是相互独立,且同服从N (0,1)分布的随机变量,则称随机变量xn2= xi2所服从的分布为x2分布。它的分布密度函数是
xi2所服从的分布为x2分布。它的分布密度函数是
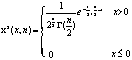
 (xk-μ)2的分布密度是:
(xk-μ)2的分布密度是: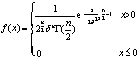
 =xp-1e-xdx。当P为自然数时Γ (n+1)=nl)。x2分布在小样本估计中具有重要作用。
=xp-1e-xdx。当P为自然数时Γ (n+1)=nl)。x2分布在小样本估计中具有重要作用。卡方分布Chi-square Distribution
概率论与统计学中常用的一种概率分布。设k个随机变量Z1,Z2,…,Zk相互独立,且都服从标准正态分布,X=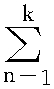 Z2n,则随机变量X被称为服从自由度为k的卡方分布,记为X~X2(k)。卡方分布常用于假设检验和置信区间的计算。
Z2n,则随机变量X被称为服从自由度为k的卡方分布,记为X~X2(k)。卡方分布常用于假设检验和置信区间的计算。
卡方分布
卡方分布
即“χ2分布”。
☚ χ分布 t分布 ☛
卡方分布
卡方分布
即“χ2分布”。
☚ χ分布 参数估计 ☛
- orissa是什么意思
- orissa pradesh是什么意思
- orissa sanskrutika parishad是什么意思
- orissa temple是什么意思
- orissa 奥里萨是什么意思
- oriya是什么意思
- orizaba是什么意思
- orizaba 奥里萨巴是什么意思
- ori服务是什么意思
- 'ork是什么意思
- orkney islands是什么意思
- orlando是什么意思
- orlando,vittorio emanuele是什么意思
- 'orld是什么意思
- orle是什么意思
- orleance:是什么意思
- orleanist monarchy是什么意思
- orleans是什么意思
- orleans,charles,duc d’是什么意思
- orleans,gaston jean baptiste, duc d’是什么意思
- orleans,louise-philippe-robert, duc d’是什么意思
- orleans,louis philippe joseph, duc d’是什么意思
- orleans,philippe ⅰ ,duc d′是什么意思
- orleans,philippe ⅱ ,duc d’是什么意思
- orleans,siege of是什么意思
- orlov,grigori grigorievich,count是什么意思
- orly 奥利是什么意思
- orléanais 奥尔良内是什么意思
- orléans charles d` 奥尔良是什么意思
- orléans gaston, duc d` 奥尔良公爵是什么意思
- orléans louis philippe, duc d` 奥尔良公爵是什么意思
- orléans maison d` 奥尔良家族是什么意思
- orléans philippe, due d` 奥尔良公爵是什么意思
- orléans 奥尔良是什么意思
- ormandy,eugene是什么意思
- orme robert是什么意思
- ormesson wladimir d是什么意思
- ormolu是什么意思
- ormonde,games butler, 1st duke of是什么意思
- ormuz 霍尔木兹海峡是什么意思
- ornament是什么意思
- ornaments是什么意思
- ornaments of bengali wives是什么意思
- ornate是什么意思
- orne 奥恩河是什么意思
- orne 奥恩省是什么意思
- ornithischie是什么意思
- ornitholestes是什么意思
- ornithology是什么意思
- ornithopoda是什么意思
- ornithopter是什么意思
- oro是什么意思
- orogeny是什么意思
- orography是什么意思
- oroide是什么意思
- orok-nilonjan是什么意思
- orontes是什么意思
- oronte 奥龙特斯河是什么意思
- orozco,jose clemente是什么意思
- orphan是什么意思