半数效量概率单位法

半数效量（或半数致死量）的概率单位法是计算半数效
量的有效方法。最先由C.I.Bliss提出，J. J. Litch-field和F. Wilcoxon根据其原理建立了图解法，顾汉颐又提出了简化概率单位法。概率单位的意义见条目“百分数的概率单位变换”。本法基本原理是将剂量反应曲线直线化，求出直线方程，再从方程求出半数效量。常用方法有：图解法、加权直线回归法和简化概率单位法，本条目将以半数致死量(LD₅₀)为例来说明。
本法要求：
❶剂量分组一般取等比级数，但也可为等差级数或不等距的数值。
❷各剂量组的受试动物数不一定相等，但应相近。
❸要求一半剂量组数的反应率在10～50%之间，其余一半在50～90%之间，尽量避免出现反应率为0%和100%。如出现反应率为0%和100%可舍去不用，或加以校正，即用“0.25÷(反应率为0%组的动物数)”代替0%，用“ 1-0.25÷(反应率为100 %组的动物数)”代替100%。
图解法 本法简便，但精确度稍差。方法步骤如下：(1)列计算表。如表1。将剂量变换为剂量对数x，死亡率变换为概率单位y。
(2) 图解求半数致死量。在方格坐标纸上，横轴为剂量对数x，纵轴为概率单位y，根据每一组的x、y值在图上描点，然后按点子的分布趋势作一直线，使直线穿过各点中间(各点至直线的纵向距离尽量短些，并重点照顾y=5附近的点子)。从纵轴概率单位为5处作一水平线，过水平线与直线的交点作垂线与横轴相交，此处读数即lgLD₅₀，取反对数得LD₅₀。
(3)求剂量反应直线方程。为更准确地求出LD₅，…，LD95等值，以及进行两直线方程的比较。可在直线上任取两点(x₁,y₁)及(x₂,y₂)，按式(1)求出直线方程

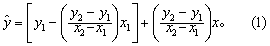
得到直线方程后，还应进行拟合优度检验，可用x₂检验。检验假设H0为实际频数符合由此直线推算出来的估计频数，即实际死亡数符合估计死亡数，实际存活数符合估计存活数。经检验，不拒绝H0则认为直线拟合好；拒绝H0则认为拟合的直线不够满意，需另行拟合满意的直线求LD50。方法步骤(如例1表2)是：
❶将各剂量对数x(死亡率为0%及100%的剂量对数除外) 代入直线方程求得估计概率单位ŷ;
❷查“百分数p与概率单位对照表”得相应的估计死亡率;
❸求相应的估计死亡数ŷ=n，估计存活数ŝ=n-;
❹由下式计算x²值，

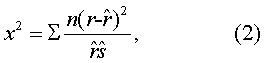
自由度ν=k-2。
k为剂量组数(死亡率为0%及100%的剂量组不计在内)。
❺查x²界值表得P值，按所取检验水准作出推断结论。
(4)求半数致死量的可信区间。上面求出的LD50是总体LD₅₀的点估计；由正态近似原理，总体LD₅₀的95%可信区间的对数值按式(3)计算，再取反对数即得LD₅₀。

式中N′为概率单位4～6范围内各组受试动物数之和。s为各致死剂量对数值的标准差，也就是回归系数的倒数，按式(4)计算：

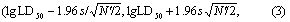
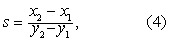
式中x₁,y₁与x₂,y₂是由图中拟合满意的直线上任意两点读出的坐标。s/为lgLD₅₀的标准误s_lgLD₅₀。例1 用某农药对雌性大白鼠作灌胃的急性毒性试验，资料见表1，用图解法求半数致死量及其剂量反应方程。
(1)列计算表。

表1 图解法求LD₅₀计算表

剂 量 mg/kg	剂量对数 x	受 试 动物数 n	死 亡 动物数 r	死亡率(%) p=r/n×100%	概率单位 y
1000 1200 1400 1600 1800	3.0000 3.0792 3.1461 3.2041 3.2553	10 10 10 10 10	1 3 7 8 9	10 30 70 80 90	3.7184 4.4756 5.5244 5.8416 6.2816

(2)用图解法求LD₅₀。

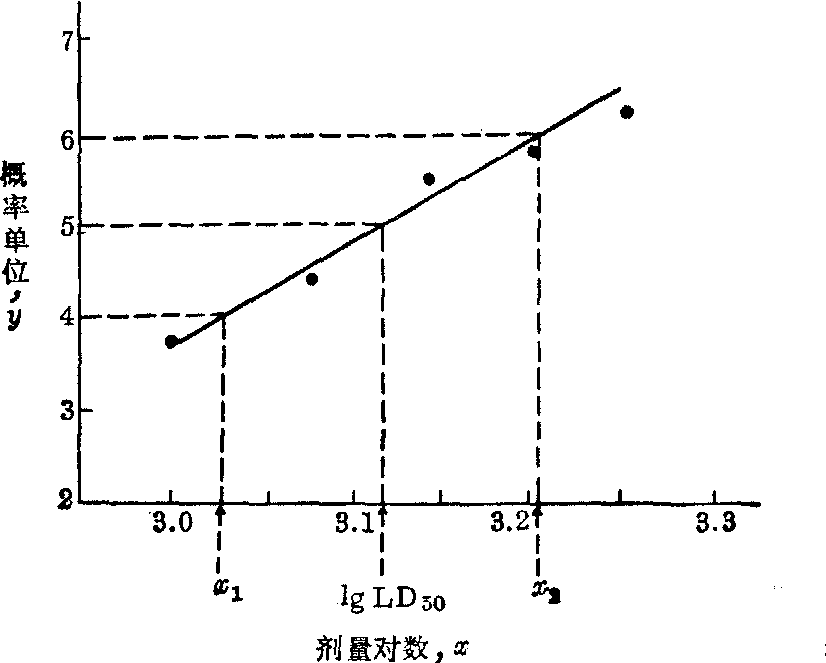
表1 资料用图解法求LD5₀

lgLD₅₀ =3.12,
LD₅0 =lg-¹ 3.12=1318(mg/kg)。
(3)求剂量反应直线方程。由图3读出线上两点： y1=4,x₁＝3.03;y2=6,x2=3.20，代入式(1)，得

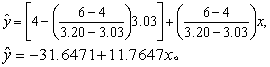
(4)拟合优度检验。
H₀: 实际频数符合估计频数，
H₁: 实际频数不符合估计频数。
α=0.05。

表2 回归直线的拟合优度检验

剂 量 对 数 x (1)	受 试 动物数 n (2)	实 际 死亡数 r (3)	估 计				n(r-)2/ ŝ (8)
			概率单位 ŷ (4)	死亡率 (5)	死亡数 (6)=(2)(5)	存 活 数 ŝ (7)=(2)-(6)
3.0000 3.0792 3.1461 3.2041 3.2553	10 10 10 10 10	1 3 7 8 9	3.65 4.58 5.37 6.05 6.65	0.09 0.34 0.64 0.85 0.95	0.9 3.4 6.4 8.5 9.5	9.1 6.6 3.6 1.5 0.5	0.01 0.07 0.16 0.20 0.53
							X2=0.91

注： 第(1)～(3)栏为原始数据，第(4)栏系将第(1)栏数据代入上述回归方程求得，第(5)栏系按第(4)栏数据由“百分数p与概率单位对照表”查得。
今v=5-2=3，查x²界值表，0.95>P>0.5，按α=0.05水准不拒绝H₀，可认为此直线拟合是好的。
(5)求LD₅₀的95%可信区间。将前述两点读数代入式(4),

由表1,N′ =30，按式(3):

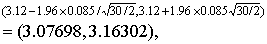
取反对数得(1194,1456)。
故此农药的LD₅₀为1318mg/kg，其95%可信区间为1194～1456mg/kg。
加权直线回归法 本法精确度高，但计算较繁。其基本思想是拟合直线时使y=5附近的数据起主导作用(给予较大的权数，详见表3)，以消除极值的影响；也考虑各组受试动物多少对死亡率稳定性的影响。方法步骤如下：(1)在图解法的基础上求出加权计算的基本数据，如表4。先用图解法求出直线方程（经拟合优度检验无显著性）。 由此求出各剂量组的估计概率单位ŷ0（取一位小数），由ŷ0查表3得加权系数w、极小值α和全距β，结合实际死亡率p ，代入式(5)求出作业概率单位y′,

y′=α+βp。(5)

求各剂量组的nw、nwx、nwx²、nwy′、nwxy′及相应的合计数∑nw、∑nwx、∑nwx²、∑nwy′、∑nwxy′。
(2)求加权直线回归方程y′=a+bx。类似条目“直线回归”方程的计算。

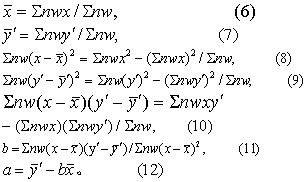
表3 加权系数

ŷ 估计概 率单位	ω 加权系数	α 极小值	β 全 距	ŷ 估计概 率单位	ω 加权系数	α 极小值	β 全 距
1.1 1.2 1.3 1.4 1.5	0.00082 0.00118 0.00167 0.00235 0.00327	0.8578 0.9521 1.0462 1.1399 1.2334	5033.84 3425.28 2354.16 1634.25 1145.89	3.1 3.2 3.3 3.4 3.5	0.15436 0.17994 0.20774 0.23753 0.26907	2.6624 2.7449 2.8261 2.9060 2.9842	15.2402 12.6662 10.6327 9.0154 7.7210
1.6 1.7 1.8 1.9 2.0	0.00451 0.00614 0.00828 0.01104 0.01457	1.3265 1.4193 1.5118 1.6038 1.6954	811.54 580.53 419.45 306.11 225.639	3.6 3.7 3.8 3.9 4.0	0.30199 0.33589 0.37031 0.40474 0.43863	3.0606 3.1351 3.2074 3.2773 3.3443	6.6788 5.8354 5.1497 4.5903 4.1327
2.1 2.2 2.3 2.4 2.5	0.01903 0.02458 0.03143 0.03977 0.04979	1.7865 1.8772 1.9673 2.0568 2.1457	167.996 126.335 95.961 73.622 57.051	4.1 4.2 4.3 4.4 4.5	0.47144 0.50260 0.53159 0.55788 0.58099	3.4083 3.4687 3.5251 3.5770 3.6236	3.7582 3.4519 3.2025 3.0010 2.8404
2.6 2.7 2.8 2.9 3.0	0.06168 0.07564 0.09179 0.11026 0.13112	2.2339 2.3214 2.4081 2.4938 2.5786	44.654 35.302 28.189 22.736 18.5216	4.6 4.7 4.8 4.9 5.0	0.60052 0.61609 0.62742 0.63431 0.63662	3.6643 3.6982 3.7241 3.7407 3.7467	2.7154 2.6220 2.5573 2.5192 2.5066

（续表）

ŷ 估计概 率单位	ω 加权系数	α 极小值	β 全 距	ŷ 估计概 率单位	ω 加权系数	α 极小值	β 全 距
5.1 5.2 5.3 5.4 5.5	0.63431 0.62742 0.61609 0.60052 0.58099	3.7401 3.7187 3.6798 3.6203 3.5360	2.5192 2.5573 2.6220 2.7154 2.8404	7.1 7.2 7.3 7.4 7.5	0.11026 0.09179 0.07564 0.06168 0.04979	-15.230 -20.597 -27.623 -36.888 -49.196	22.736 28.189 35.302 44.654 57.051
5.6 5.7 5.8 5.9 6.0	0.55788 0.53159 0.50260 0.47144 0.43863	3.4220 3.2724 3.0794 2.8335 2.5229	3.0010 3.2025 3.4519 3.7582 4.1327	7.6 7.7 7.8 7.9 8.0	0.03977 0.03143 0.02458 0.01903 0.01457	-65.678 -87.928 -118.212 -159.782 -217.335	73.622 95.961 126.335 167.996 225.639
6.1 6.2 6.3 6.4 6.5	0.40474 0.37031 0.33589 0.30199 0.26907	2.1325 1.6429 1.0295 0.2606 -0.7051	4.5903 5.1497 5.8354 6.6788 7.7210	8.1 8.2 8.3 8.4 8.5	0.01104 0.00828 0.00614 0.00451 0.00327	-297.71 -410.96 -571.95 -802.87 -1137.13	306.11 419.45 580.53 811.54 1145.89
6.6 6.7 6.8 6.9 7.0	0.23753 0.20774 0.17994 0.15436 0.13112	-1.9214 -3.4589 -5.4111 -7.9026 -11.1002	9.0154 10.6327 12.6662 15.2402 18.5216	8.6 8.7 8.8 8.9 9.0	0.00235 0.00167 0.00118 0.00082 0.00057	-1625.39 -2345.20 -3416.23 -5024.70 -7462.92	1634.25 2354.16 3425.28 5033.84 7472.15

本表按下式算得：估计概率单位ŷ=u+5,w=z²
/P(1-P),a=ŷ-P/z,β=1/z。其中u为标准正态变量，相应的标准正态曲线的纵坐标为z、左侧面积为P。
(3)按式(13)可求任何死亡率(k%)时的致死剂量对数(lgLD_k)，按式(14)求其标准误(slgLD_k)。按式(15)求LD_k的95%可信区间的对数值，取反对数即得真数值。

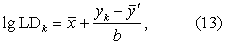
式中yk为死亡率k%相应的概率单位。

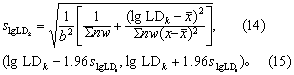
如此，由第一轮加权求得的直线回归方程常有较大误差，特别是在计算LD₅和LD₉₅时更是如此。故应采用多轮加权，逐次逼近。每轮均以所得方程的应变量估计值，作为下一轮加权的估计概率单位。仿上法重复进行，直到各剂量组前后估计概率单位之差均不超过0.2时即算满意。
例2 对例1资料用加权直线回归法求LD50。(1) 由例1图解法求得初估的剂量反应回归方程为
ŷ₀＝-31.6471+11.7647x。
❶
由此借助表4求出加权计算的基本数据：

表4 加权计算的基本数据

剂量对数 x (1)	动物数 n (2)	死亡率 p (3)	估 计 概率单位 ŷ0 (4)	加权系数 ω (5)	极小值 α (6)	全 距 β (7)	作 业 概率单位 y' (8)	估计概率单位
								1 (9)	2 (10)
3.0000 3.0792 3.1461 3.2041 3.2553	10 10 10 10 10	0.1 0.3 0.7 0.8 0.9	3.6 4.6 5.4 6.0 6.7	0.30199 0.60052 0.60052 0.43863 0.20774	3.0606 3.6643 3.6203 2.5229 -3.4589	6.6788 2.7154 2.7154 4.1327 10.6327	3.7285 4.4789 5.5211 6.8291 6.1105	3.8 4.6 5.3 5.9 6.4	3.8 4.6 5.3 5.9 6.4

注：表4第(1)～(3)栏为原始数据，第(4)栏由上述直线回归方程式
❶求得，第(5)～(7)栏由表3查得，第(8)栏由式(5)算得，第
(9)栏由第一轮加权直线回归方程式
❷算得，第(10)栏由式
❸求得。

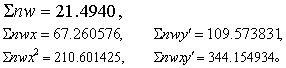
(2)按式(6)～(12)求加权直线回归方程。

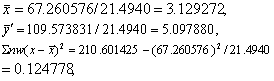
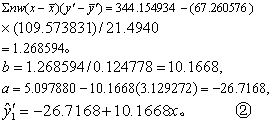
将表4第(1)栏数据代入上式得第(9)栏，第(4)栏与第(9)栏比较，最高剂量组y0-y1=6.7-6.4=0.3，尚不够满意；为此重复上述步骤作第二轮加权计算（过程从略），得回归方程

＝-27.5231+10.4272x。
❸

将表4第(1)数据代入上式得第(10)栏。第(9)栏与(10)栏比较完全一致，说明式
❸直线拟合已很满意。
(3)求LD₅₀及其95%可信区间。在第二轮计算中已求得：∑nw=23.6035,∑nw(x-)²＝0.152906,＝3.131714,
＝5.131933。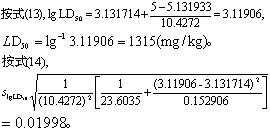

按式(15),
(3.11906-1.96×0.01998,3.11906+1.96×0.01998)=(3.07990,3.15822)，取反对数得(1202,1440)。
故此农药的LD₅₀为1315mg/kg，其95%可信区间为1202～1440mg/kg。
简化概率单位法 本法计算简单且较精确，适于2～5个剂量组，剂量分组取等比级数排列，每组动物数相同，一般用10～20只动物，较大动物每组至少也宜有5只。lgLD₅₀及其标准误的算式随剂量组数不同而异。
二个剂量组：

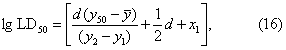
式中d为相邻两剂量对数值的差值，y₅₀＝5。
例3 用某农药对雌性大白鼠作灌胃的急性毒性试验，结果见表5。用简化概率单位法求LD₅₀。

表5 简化概率单位法计算表

剂 量 mg/kg (1)	剂量对数 x (2)	受试动物数 n (3)	死亡动物数 r (4)	死亡率 p (5)	概率单位 y (6)	加权系数 w (7)	权 数 nw (8)
932 1086 1265 1473	2.9694 3.0357 3.1020 3.1683	10 10 10 10	1 2 5 7	0.1 0.2 0.5 0.7	3.7184 4.1584 5.0000 5.5244	0.3359 0.5026 0.6366 0.5810	3.359 5.026 6.366 5.810
1716	3.2346	10	9	0.9	6.2816	0.3359	3.359
					24.6828		23.920

注： 第(1)～(5)栏为原始数据，第(6)栏是按第(5)栏由“百分数p与概率单位对照表”查得，第(7)栏由表(3)查得。
列表5。 本例有五个剂量组，d=0.0663, ＝∑y/组数=24.6828/5=4.9366。

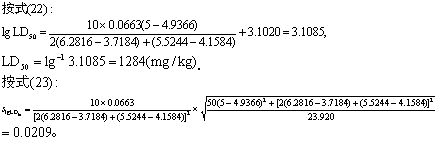
按式(15)求LD₅₀的95%可信区间的对数值：
(3.1085-1.96×0.0209,3.1085+1.96×0.0209)=(3.0675,3.1495),
取反对数得(1168,1411)。
故此农药的LD₅₀为1284mg/kg，其95%可信区间为1168～1411mg/kg。