匹配滤波与维纳滤波

匹配滤波与维纳滤波都是从背景噪声中提取信号的方法。匹配滤波是从背景噪声中检测已知信号是否存在的有效手段，其作用不在于防止信号波形的失真，而在于提高某一时刻输出的信噪比。维纳滤波是在信号和噪声都是随机量，其功率谱在互相交迭情况下，从某种最优意义上提取信号的方法。
匹配滤波 设输入量x(t)是由信号S_i(t)和噪声n_i(t)相加组成，由于噪声较强而难以通过直接观测x(t)波形来判断信号S_i(t)是否存在； 当使x(t)通过匹配滤波器后，其输出量y(t)=S₀(t)+n₀(t)中的信号输出S₀(t)可在t=T₀时刻达到最大(T0为信号S_i(t)持续期的终了)，如果在此瞬间对输出采样，则能使采样输出y(T₀)=S₀(T₀)+n₀(T₀)中的信号分量S₀(T₀)尽可能大，于是提高了瞬时信噪比，且根据此采样结果可检测信号是否存在。
当输入信号S_i(t)已知，而输入背景噪声n_i(t)为白噪声时，设计匹配滤波器的原则是使滤波器的幅频特性与信号的幅频特性相同，而其相频特性与信号的相频特性相反，并具有使波形延迟T0秒所需的线性相位因子，如图1所示。从时域上看，匹配滤波器的冲激响应波形应是输入信号波形的首尾倒置，如图2所示。当已知信号S_i(t)的频谱为F_Si(f)，而背景噪声为白噪声时，匹配滤波器的频率特性为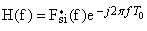
(*表示共轭)其冲激响应为

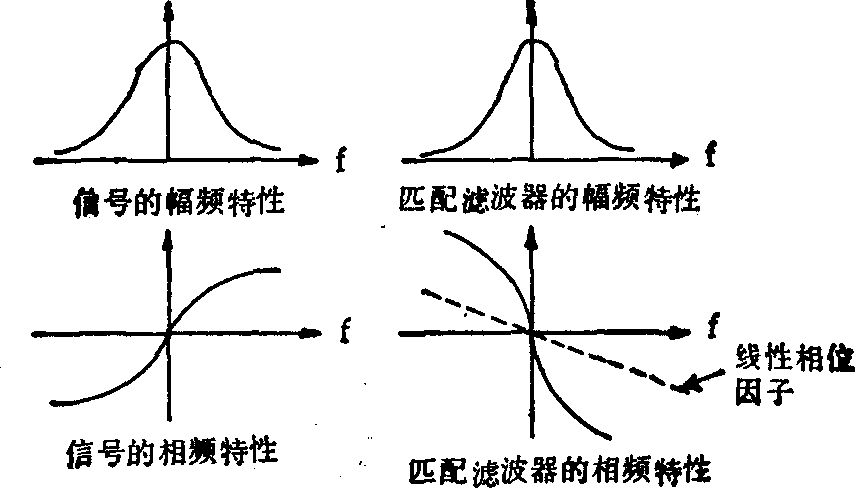
图1 匹配滤波器的频率特性

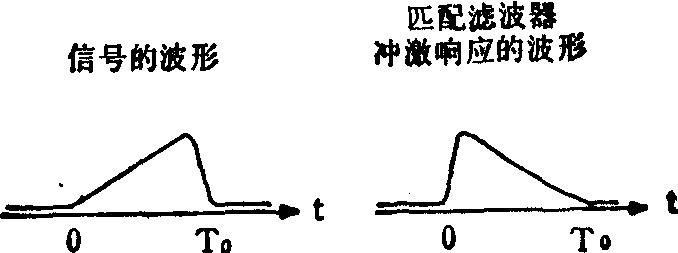
图2 匹配滤波器的冲激响应

h(t)=S_i(T₀-t),T₀为S_i(t)的持续时间
经过匹配滤波器后的信号输出波形与原信号波形不同，但当信号间歇出现时，可利用匹配滤波器的输出波形判断信号来临的大致时刻，以便从输入波形中把含有信号的时段截取出来。例如，脑电图在其基本韵律的背景下会不时发生一些瞬态，即一些有别于背景韵律的，持续时间较短而幅度较大的脉冲，它们往往起源于一些生理干扰（如眼球运动等），而不是所关心的特征，应在计算机处理时去除，以免引起假象。为此，可从一段脑电图上找到典型瞬态（称模板），以它为根据建立匹配滤波器，然后使实测脑电通过此滤波器。当某时刻(例如A)滤波器输出超过阈值时，则可判断这段脑电图中含有瞬态，于是将模板与这段脑电图相减，便能消除瞬态，如图3所示。实际信号的波形往往不能预知。这时可先根据经验拟定一初始信号模板，并借此检测出含有信号的时段，然后再用这些时段修改初始模板。随着检测过程不断更新模板，即可不断改进模板的可靠程度，又可自动跟随信号的非平稳变化。

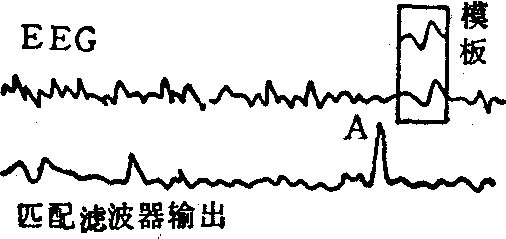
图3 消除脑电图中瞬态干扰的方法

维纳滤波 维纳滤波是一种线性最小均方滤波器。设观察值x(t)由信号S(t)和噪声n(t)相加组成，δ(t)是希望得到的处理结果，则x(t)经线性处理后得到的输出(t)是δ(t)在最小均方误差意义下的逼近，即∫〔δ(t)-(t)〕2dt=极小，按此原则设计出的线性处理器便是维纳滤波器，如图4所示。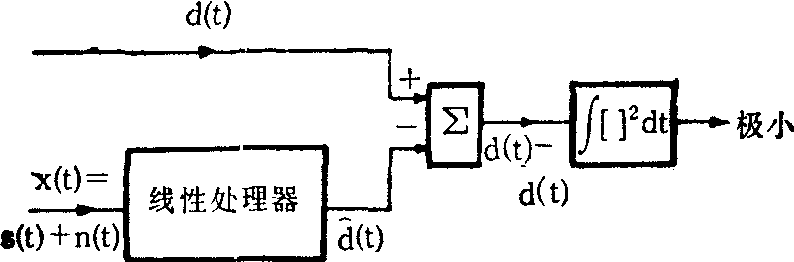

图4 维纳滤波器

维纳滤波器的频率特性H(f)为H(f)=Ss(f)/Ss(f)+Sn(f)式中Ss(f)是信号的功率谱(参见“信号的谱分析”条),Sn(f)是噪声的功率谱。如果信号和噪声两项特性已经预知，就可据以设计维纳滤波器，用于离线处理。如果信号和噪声的功率谱或相关函数特性未知，就需要作出它们的估计，然后利用上式进行滤波器设计，这种滤波器被称为后验维纳滤波器。有人用后验维纳滤

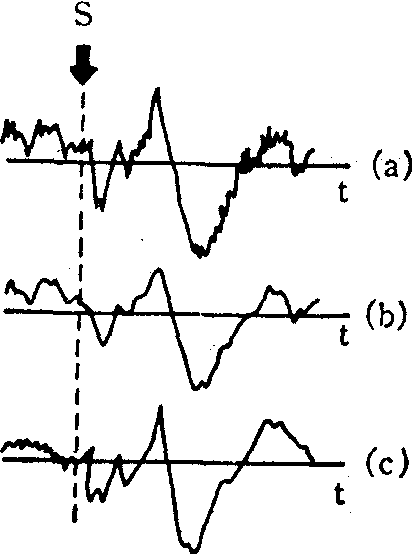
图5用后验维纳滤波器处理诱发响应

波来处理诱发响应，以便减少提取诱发响应所需要的累加次数，如图5所示。(a)表示躯体感觉诱发电位经20次累加后的平均响应。(b)表示对(a)的后验维纳滤波结果。(c)图是直接作200次累加的结果。