包络定理
包络定理envelope theorem
最早在1931年由瓦伊纳(J.Viner)和王(Y. K. Wong)在讨论短期和长期平均成本曲线之关系时提出的,他们认为:长期平均成本曲线不仅总低于短期成本曲线,且通过每一条短期成本曲线的最小点。后来在1947年萨缪尔森(Samuelson)用一般方法证明,长期成本曲线就是短期成本曲线族的包络。考虑一个含单参数a的函数f(x,a)的无条件极值问题minf(x,a)。
对每一个a,上问题的解记为x(a),设最小值f(x(a),a)=M(a),则随着a的变化M(a)也变动。对M(a)关于a求导数得:
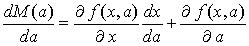
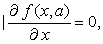 从而上式变为:
从而上式变为: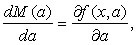
对含参数a的带约束条件极值问题:
minf(x1,…,xn,a)
s. t.g(x1,…,xn,a)=0
令拉格朗日函数L=f(x1,…,xn,a)-λg(x1,…,xn,a),对每一个a,上问题的解为x1(a),…,xn(a),记f(x1(a),…,xn(a),a)=M(a)。类似于上面的做法得: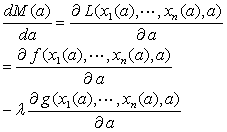
☚ 凸性 不动点定理 ☛
- 㗳是什么意思
- 㗳舌弄舌是什么意思
- 㗴是什么意思
- 㗵是什么意思
- 㗷是什么意思
- 㗻是什么意思
- 㗼是什么意思
- 㗾是什么意思
- 㗾哆是什么意思
- 㗿是什么意思
- 㘁是什么意思
- 㘃是什么意思
- 㘄是什么意思
- 㘄哏儿是什么意思
- 㘆是什么意思
- 㘆𠷂讲是什么意思
- 㘈是什么意思
- 㘈㘈是什么意思
- 㘉是什么意思
- 㘊是什么意思
- 㘊霵是什么意思
- 㘋是什么意思
- 㘎是什么意思
- 㘐是什么意思
- 㘑是什么意思
- 㘓是什么意思
- 㘔是什么意思
- 㘖是什么意思
- 㘗是什么意思
- 㘗㘗是什么意思
- 㘗㘗哝哝是什么意思
- 㘗㘗话是什么意思
- 㘗咕是什么意思
- 㘗咕嚓咕是什么意思
- 㘗箅是什么意思
- 㘙是什么意思
- 㘚是什么意思
- 㘛是什么意思
- 㘝是什么意思
- 㘞是什么意思
- 㘞底是什么意思
- 㘠是什么意思
- 㘢是什么意思
- 㘣是什么意思
- 㘤是什么意思
- 㘥是什么意思
- 㘥子是什么意思
- 㘦是什么意思
- 㘧是什么意思
- 㘩是什么意思
- 㘪是什么意思
- 㘪土是什么意思
- 㘭是什么意思
- 㘰是什么意思
- 㘱是什么意思
- 㘵是什么意思
- 㘿是什么意思
- 㙀是什么意思
- 㙁是什么意思
- 㙂是什么意思