勾股数

 今有二人同所立。甲行率七，乙行率三。乙东行。甲南行十步而邪东北与乙会。问甲、乙行各几何？
 术曰：令七自乘，三亦自乘，并而半之，以为甲邪行率。邪行率减于七自乘，馀为南行率。以三乘七为乙东行率。置南行十步，以甲邪行率乘之。副置十步，以乙东行率乘之，各自为实。实如南行率而一，各得行数。
 

汉《九章算术·勾股》

 【评】此为《九章算术》极其重要的一个题目。它实际上提出了世界上第一个勾股数组通解公式：

a:b:c=[m²-(m²+n²)]:mn:(m²+n²)

,
 其中m,n互素的条件，在实际上是满足的。古希腊的柏拉图、欧几里得等只提出了某些特殊情形。公元三世纪丢番都提出了与《九章算术》类似的公式，晚出三百馀年。
 今有邑方一十里，各中开门。甲、乙俱从邑中央而出。乙东出；甲南出，出门不知步数，邪向东北磨邑隅，适与乙会。率：甲行五，乙行三。问甲、乙行各几何？
 术曰：令五自乘，三亦自乘，并而半之，为邪行率。邪行率减于五自乘者，馀，为南行率。以三乘五，为乙东行率。置邑方半之，以南行率乘之，如东行率而一，即得出南门步数。以增邑方半，即南行。置南行步，求弦者，以邪行率乘之；求东行者，以东行率乘之，各自为实。实如南行率，得一步。
 

《九章算术·勾股》

 【评】此术与上术同，亦提出了勾股数通解公式，正如刘徽指出的：“求三率之意与上甲、乙同”。这再一次表明，《九章算术》实际上掌握了勾股数该通解公式的一般形式。
 此以南行为勾，东行为股，邪行为弦。并勾弦[原本脱“弦”字，依意补]率七。欲引者，当以股率自乘[原本脱此四字，依意补]为幂，如并而一，所得为勾弦差率[原本脱“率”字，依意补]。加并，之半为弦率，以差率减[原本脱“弦”、“差”二字，参考戴震补],馀为勾率。如是或有分，当通而约之乃[原本讹作“及”,戴震校]定。术以勾弦并率[此四字原本讹作“可使”,依钱宝琮校]为分母，故令勾弦并自乘为朱、黄相连之方。股自乘为青幂之矩，以勾弦并为袤，差为广，今有相引之直，加损同上。其图[原本讹作“圆”,戴震校]大体，以两弦为袤，勾弦并[此二字，大典本讹作“股”,戴震校]为广。引横断其半为弦率，列用率七自乘者，勾弦并之率，故弦减之，馀为勾率。同立处是中停也，皆勾弦并为率，故亦以勾率同其袤也。南行十步者，所有见勾求见弦、股，故以弦、股率乘[原本脱“乘”字，李潢补],如勾率而一。
 

《九章算术·勾股》三国魏·刘徽注

 【评】刘徽分别用解析方法和出入相补原理，对《九章算术》的勾股数公式作了证明，是为世界数学史上第一次证明。此注系于“二人同所立”问之下。
 法曰：勾弦和自乘，股率自乘，并而半之，为弦；以减和求勾，股率乘勾弦和率求股^①。以所有勾数乘所求勾、股、弦三率为列实，以所有勾率为法，除之。
 

《九章算术·勾股》宋·贾宪细草(《宜稼堂丛书》本杨辉《详解九章算法》)

 【评】此为贾宪对求勾、股、弦三率(即勾股数通解公式)的进一步抽象。
 以三率之中率为主，倍中率为股，首末二率相减为勾，相加为弦。
 

清·王元启《勾股衍·答友问勾股书》

 【评】此实际上给出勾、股、弦三率为：

勾股数Gougushu

在西方称为毕达哥拉斯数，即不定方程
x²+y²＝z² (1)
的正整数解， 几何意义为边长均是正整数的直角三角形。在古代， 有时也取正有理数解。
初等数论中有如下定理：不定方程(1)的适合x>0, y>0, z>0, (x, y) =1, 2|x的解， 必可表示为
x=2ab, y=a²-b², z=a²+b²
(a, b) =1, a>b>0, a、b一奇一偶的形
式， 且如此的 (x, y, z)与自然数对 (a, b) 一一对应。
寻求边长均为正整数或正有理数的直角三角形，这一问题在数学发展的早期曾先后引起过巴比伦、希腊、印度、中国， 可能还有埃及等各古代民族的注意。埃及人给出了最简单的一组勾股数(3,4,5)。在成书于公元前8——前5世纪的印度的《祭坛建筑》中不仅记载了勾股定理，而且记载了6组勾股数：3,4, 5:5.12, 13; 7. 24, 25; 8, 15, 17; 12, 35, 37; 15, 36,39。说明他们在那时已经有了求勾股数的某种方法。实际上， 这6组勾股数均可归入两个互补的模式
x: y: z=2a: (a²-1): (a²+1) (2)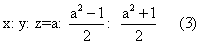
在公元前5——前4世纪， 希腊的毕达哥拉斯学派和柏拉图学派也给出了这两个公式。
在一块属于公元前1900——前1600年间的古巴比伦泥板上，记载着令人惊叹的数学内容。它曾是普林顿(Plimpton,G. A.)的个人收藏品，现存美国哥伦比亚大学图书馆，编号为322，因而被称为“普林顿322号泥板” （如图）。

普林顿322号泥板
泥板的左半部分已经遗失，右半部分用巴比伦的 60 进位值制刻着 4 列、15 行数字。若按
从左至右的顺序把这4列数字分别标为A、B、C、D，则D为行的序号，从1直到15;B、C的意义为：若把勾股数公式写为

x=2ab, y=a²-b², z=a²+b²

则B、C列中的数分别对应于y、z;A列则对应于
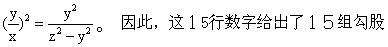
数。如果把A列用相应的x值代替，并给出与(x,y,z)相应的参数组(a,b)，就可以列出下表（用今天的数码）:

x	y	z	a	b	序号
120 3 456 4 800 13 500 72 360 2 700	119 3 367 4 601 12 709 65 319 2 291	169 4 825 6 649 18 541 97 481 3 541	12 64 75 125 9 20 54	5 27 32 54 4 9 25	1 2 3 4 5 6 7

x	y	z	a	b	序号
960 600 6 480 60	799 481 4 961 45	1 249 769 8 161 75	32 25 81	15 12 40	8 9 10 11
2 400 2 40 2 700 90	1 679 161 1 771 56	2 929 289 3 229 106	48 15 50 9	25 8 37 5	12 13 14 15

第11行在60进位值制中的意义实际应为
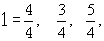
相应于勾股数(3,4,5)，参数组为(2.1)。这15组勾股数，既不可能是通过试验的方法得到的，也无法归入任何特殊的模式，因此，它说明当时巴比伦人很可能已经掌握了推求勾股数的一般公式。
在希腊，欧几里得在《几何原本》中给出了今天的勾股数公式的等价形式，并严格地证明了它。在中国，《九章算术》勾股章中给出了与今天的公式完全一致的形式， 严格的证明是在公元3世纪由刘徽明确地给出的。
公元3世纪，丢番图在他的《算术》中重新叙述了欧几里得已研究过的勾股数问题：“把 一给定的平方数分解为两个平方数”。由于他研究的是正有理数解而不限于整数， 上述问题实际上与一般勾股数问题是完全一致的。大约在1636年，这个问题被法国大数学家费尔马进一步研究， 提出
xⁿ+yⁿ＝zⁿ n>2
没有正整数解，即著名的费尔马大定理（参见该条），对后世数学的发展产生了深远的影响。