加总问题problem of aggregation

由于总量数据是由个量数据加总而成，但加总过程并非简单汇总，而是在个量数据基础上经过加工处理才得到总量数据。无论在哪一个汇总层次上作处理，其结果必定是使所得的宏观数据不再等于微观数据的简单总和。比如t期有n个家庭，每个家庭的消费函数是：

c_i＝α_i+β_iy_i(i=1,2,3，…n)

其中c_i、y_i分别表示第i个家庭在t时期的消费支出与收入。α_i为当收入为0时的消费支出，β_i为边际消费倾向。若将n个家庭的消费函数进行简单的加总，则得：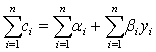

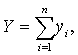对于n个家庭其总收入总消费支出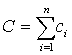时作的宏观模型为：

C=α+βY

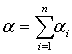此时含义清楚，但βY何时与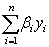相等？只有两种情况：
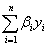
一种是，当β=β₁＝β₂＝…=β_n时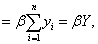，但这非常理想化，因为所有家庭的边际消费倾向不太可能都相同。
另一种是，β可解释为加权平均，即β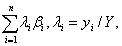^*＝此时：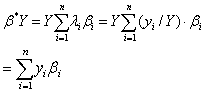

但由于λ_i将随收入分布而变化，使β^*不是常数，这与β意义不符，总之，加总后对真实的微观模型将产生偏离。Theil讨论了使期望偏离最小的加总，谓之最优加总。近年来，从个量过渡到总量所遇到的理论问题也是研究领域活跃的问题。