刺激三要素及其相互关系
刺激三要素及其相互关系
每一刺激都包含有三种要素,即强度、持续时间以及强度变化率(即坡度或梯度)。把三者间的关系绘制成三维空间的六面立方体,叫做刺激阈立体,可以全面地表达刺激三要素之间的各种关系。
强度-时间曲线及Weiss式以电刺激为例,当电流强度变化率固定时,把引起兴奋所需要的电流强度i和它所需要的持续时间t的关系,绘成曲线,叫做强度-时间曲线。刺激强度越小,越需要延长持续时间才能产生兴奋,二者的关系形成一条双曲线(图1)。
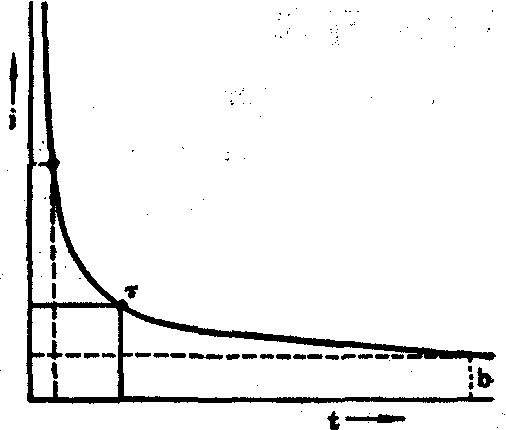
图1 强度-时间曲线
Hoorweg(1892)、Weiss(1901)把这一曲线制成实验式,一般叫做Weiss式。

i为电流强度; t为持续时间;a及b是常数。移项

两项应有一个共同数,假设它为I,则
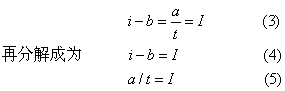
式4确定了i可以分成I及b。为了证明二者确实可分,而且可以各自反映不同的物质变化,这里借用Lucké等(1935)就实物所做的工作,加以类比。Lucké等曾作过与某种海生动物卵的渗透压有关的工作,得出的公式
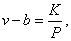
恰好在形式上和Weiss式(2)完全一致,并可仿式(4)假设v-b=V。
K是常数,P是压力,v是总容积,b是渗透迟钝物质,V是从总容积减去渗透迟钝物质所余的物质,说明总容积v可分为两种不同物质b及V。以Lucké等的工作为类比,可以说明两个问题。其一,可以说明我们提出的i可分为I及b不是人为的,它和v可分为V及b一样是确实可分的; 另一方面也应当推论,Weiss式中的I及b也和Lucké工作中的V及b一样,应该是反映被刺激的对象在反应过程中产生了两种不同的物质变化,或者是同一物质的不同形式的变化。
时值 Lapicque(1909)提出:用无限长的持续时间,刺激神经肌肉等可兴奋组织时,为了引起兴奋所需要的最小电流强度,叫做基强度。用二倍基强度的电流强度,为了引起兴奋所需要的最短持续时间,叫做时值,用τ来表示。他并认为时值是用时间因素来反映兴奋性的指标。在Weiss式上他假定i=2b,代入式中则为:
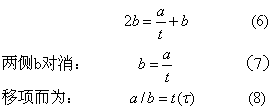
利用时与刺激阈的关系 在某一强度情况下,为引起组织兴奋所需要的最短持续时间称利用时 (Gildeme-ister,1908);时值实质上是在二倍基强度情况下求得的利用时。在用基强度的刺激强度情况下,为了引起组织兴奋所需要的最短持续时间,叫做主利用时。利用时和强度阈(刺激阈)之间的关系:根据“在同一平面上两个坐标规定一个点”的定理来看,在强度-时间曲线上二者是同一个点,只是由于用不同坐标来观测,乃提出了两个不同的名称。亦即从横坐标看是利用时的那个点,从纵坐标上看就是强度阈值(用强度所表达的刺激阈值)。这一点过去常被人们所忽视。所以Lapicque特别强调时值是用时间因素来反映组织兴奋性的论点,是不够正确的。
适应曲线及强度-坡度曲线 当用电流刺激组织时,刺激电流的坡度(即上升速度)越小,刺激阈越升高,这种现象就叫做适应。当坡度过小时,则完全不能引起组织兴奋,这种现象叫做潜入。也就是坡度越小,越需要加强刺激强度才能引起兴奋。坡度小到刚好用任何强大的电流也不能引起兴奋时,称最小坡度。Solandt (1936年,在Hill指导下)用二倍基强度的电流强度刺激神经,观察刚好不能引起兴奋所需要的坡度上升时间R·C,用以反映坡度(R是电阻,C是电容,1/R·C是坡度,R·C越大,坡度越小),用λ来表示它,并命名为适应常数。用同样的方法,在三倍、四倍、五倍基强度时测定这一坡度上升的时间,连接成线,叫做适应曲线(图2)。为了建立刺激阈立体,我们提出强度-坡度曲线,用以反映强度与坡度之间的关系。它与适应曲线的区别在于适应曲线是在分别用二倍、三倍、四倍、五倍基强度情况下求得各自刚好不能引起兴奋所需要的用R·C所表达的坡度,而强度-坡度曲线则是在与上述相同条件下求得几个刚好引起兴奋所需要的用R·C所表达的坡度所连结的曲线。
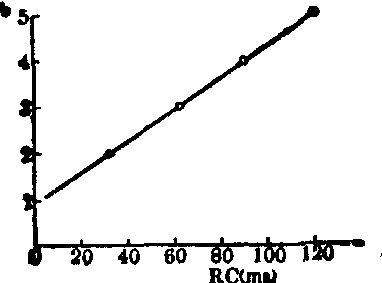
图2 适应曲线
坡度-时间曲线 在一定的电流强度下(当时作者用的是二倍基强度)为了引起兴奋,电流持续时间和坡度之间有一定关系,绘成曲线叫做坡度-时间曲线,形状很近似滴定曲线(图3)。因为是在二倍基强度的电流强度下求得的曲线,所以在时间坐标上曲线起始于τ,在坡度坐标上曲线终止于λ。充分说明λ是用R·C反映坡度的,而不是时间因素。还可看出τ、λ不在同一坐标上。其次,在这一曲线上还可看到一个临界时间,在这一时间的以前和以后的坡度变化极为显著。犹似在滴定曲线上稍加一些指示剂,颜色就起骤变的情况,也很象Hodgkin所叙述的那样: 缓慢上升的电流引起的去极化是逐渐增加的,这时会使钠运载系统失活。这一时间的生理学意义有待于进一步研究。
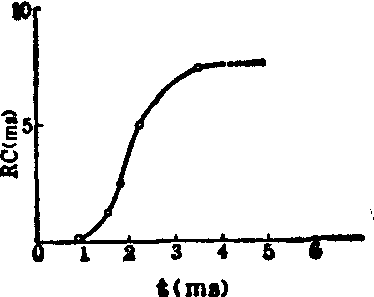
图3 坡度-时间曲线
刺激阈立体 是反映刺激三要素相互之间的关系,由上述三条曲线所构成 (图4)。从刺激阈立体可以清楚地看到强度-时间曲线是在用直角电流情况下求得的强度与时间的关系。强度-坡度曲线是在持续时间为无限长的情况下求得的强度与坡度关系 (因为基强度是在持续时间为无限长的情况下求得的)。坡度-时间曲线是在固定一定强度情况下求得的时间与坡度的关系,不是没有电流强度,在刺激中三要素少一个也不行。时值τ是在用直角电流二倍基强度情况下求得的时间,而λ虽然是用时间来表达,但实质上它是在持续时间为无限长,二倍基强度情况下求得的刚好不引起组织兴奋所需要的用时间R·C所表达的坡度。
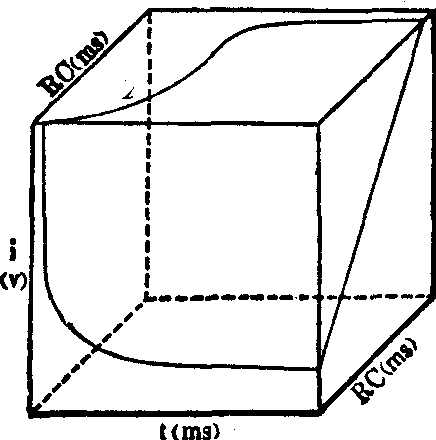
图4 刺激阈立体
☚ 刺激与兴奋 应激性和兴奋性 ☛
- 三陵使、副使是什么意思
- 三陵地是什么意思
- 三陵官地是什么意思
- 三陵总理事务大臣是什么意思
- 三陵遗址是什么意思
- 三陵都监是什么意思
- 三陷是什么意思
- 三陷证是什么意思
- 三陽是什么意思
- 三陽五會是什么意思
- 三陽卦是什么意思
- 三隅灶是什么意思
- 三隅竈是什么意思
- 三隅自反是什么意思
- 三階是什么意思
- 三障是什么意思
- 三隧是什么意思
- 三隻手是什么意思
- 三隻虎鉞是什么意思
- 三难是什么意思
- 三难推理是什么意思
- 三难苏学士是什么意思
- 三难轩是什么意思
- 三难轩质正是什么意思
- 三难顺风旗是什么意思
- 三雀观是什么意思
- 三雅是什么意思
- 三雅之爵是什么意思
- 三雅园斗蟋蟀是什么意思
- 三雅斋是什么意思
- 三雅杯是什么意思
- (三)雅的中心在于培养内德是什么意思
- 三雍是什么意思
- 三雍宫是什么意思
- 三 雕版印刷术和活字印刷术是什么意思
- 三 雨山区是什么意思
- 三雪接骨粉是什么意思
- 三雲帖是什么意思
- 三雲殿是什么意思
- 三霄是什么意思
- 三 霍邱县是什么意思
- 三霜是什么意思
- 三靈是什么意思
- 三靈之流是什么意思
- 三青两黄是什么意思
- 三青四绿是什么意思
- 三青团是什么意思
- 三青团始末是什么意思
- 三青子是什么意思
- 三青蔓是什么意思
- 三青鸟是什么意思
- 三靠是什么意思
- 三靠臂是什么意思
- 三面是什么意思
- 三面下锯法是什么意思
- 三面临水的陆地是什么意思
- 三面人是什么意思
- 三面八臂观音浮雕是什么意思
- 三面六目是什么意思
- 三面刀儿四面斗儿是什么意思