刚体定轴转动gangti dingzhou zhuandong

刚体内始终有一直线保持不动的运动。这根固定直线称为刚体的转轴。图1中固定平面π相对参照系静止，转动平面s与刚体固连，两平面的交线与转轴重合，可以用由π面到s面的转角去描述刚体的位置。转角ᵠ是代数量，规定由转轴oz正端看刚体，ᵠ角由π面逆时针转到s面时为正，反之为负。角位移是转角ᵠ在一段时间间隔内的改变量。设刚体由t₁时刻的转角ᵠ变化到t2时刻的转角ᵠ2，在时间间隔△t=t₂-t₁内刚体的角位移为△ᵠ=ᵠ2-ᵠ1。角位移△ᵠ与它对应的时间间隔△t的比值＝△ᵠ/△_t称为刚体在时间△t内的平均角速度。它描述了刚体在这段时间内角位移的平均变化情况，也是刚体转动快慢的平均值。当时间间隔△t趋向零时，平均角速度的极限为，它描述了刚体在某一时刻转动的快慢和方向，称为刚体作定轴转动时的瞬时角速度，简称角速度。角速度ω是一个代数量，其正负号可以区别刚体的不同转向。由转轴oz正端看刚体，如果刚体逆时针转动，则ω为正值，反之为负值。角速度的单位是弧度/秒(rad/s)。在工程中，刚体转动快慢常用每分钟转若干转表示，以n代表。n与ω的关系为：ω=2πn/60弧度/秒。角加速度是描述刚体角速度变化快慢的物理量。设在时刻t₁和t₂刚体的角速度分别为ω₁和ω2,△ω=ω₂-ω₁为在时间间隔△t=t₂-t₁内刚体角速度的改变量。△ω与△t的比值△ω/△t称为平均角加速度，其极限，称为刚体的角加速度，表示在某一时刻刚体角速度的变化情况。α是代数量，数值由角速度的时间变化率dω/dt决定。当ω>0,α>0，或ω<0,α<0时，刚体作加速转动；当ω>0,α<0，或ω<0,α>0时，刚体作减速转动；当α=0,ω=常数时，刚体作匀角速转动，如果ω=0，刚体不转动。角加速度的单位是弧度/秒²(rad/s²)。转动刚体内各点都分别在自身所在的与转轴垂直的平面内作圆周运动，圆心在转轴上。在同一瞬时，它们有着共同的角速度和角加速度，但其速度和加速度不尽相同。如果刚体的角速度为ω，刚体内某点的转动半径为R，则该点速度的大小等于角速度与转动半径的乘积，即v=Rω，速度的方向与该点的运动方向一致。如果刚体的角加速度为α，刚体内一点的切向加速度等于该点的转动半径与角加速度的乘积αi=Rα；法向加速度等于转动半径与刚体角速度平方的乘积，α_n＝Rω²。总加速度的大小α=R，其方向可由总加速度与半径的夹角ᵠ决定，tgᵠ=α/ω²在任一瞬时，转动刚体内所有各点速度和加速度的大小都与各点转动半径R成正比，离转轴越远的点，速度和加速度都越大。在任一瞬时，刚体内所有各点的加速度对其转动半径的偏角都相同。

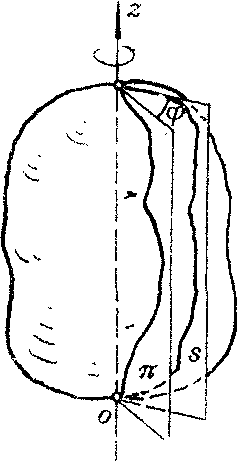
图1

图2