分数法

用于单因素取值范围是不连续情况的一种优选方法。它是由斐波那契数列构造一个分数数列 〔Gn〕：1/1,1/2,2/3,3/5,5/8,8/13,13/21,21/34,34/55……，用它代替0.618。这串分数从第二项起，每个分数的分子是其前面一个分数的分母，而其分母则为前一个分数的分子与分母之和。这列分数任一项近似等于0.618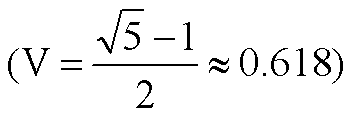，分数法就是按实际问题需要来适当选取一个分数，再按黄金分割法同样步骤进行优选。具体程序如下： (1) 确定实际问题某因素的取值范围的全部离散值。(2) 在分数数列〔G_n〕 中找分母大于最大离散值的最小项G_n，最小项G_n是第几项，就试验第几次。(3) 将第一个试验点取在G_n的分子上。(4) 按黄金分割法确定以后各个试验点。下一个试验点C₂＝ （左端点） + （右端点）-（保留点）。继续照此进行试验，直至取得最优方案。例如某产品的加工质量关键取决于热处理炉的控制温度。根据分析，合格产品温度控制有12级(从850℃开始，每升高5℃为一级，直至905℃)。怎样用分数法优选最佳控制温度？ 因为温控离散值最大为12级、故在分数数列中挑选8/13 （即第五项），确定试验五次。第一试验点： C₁在温控八级上885℃进行试验。第二试验点： C₂＝(1+12)-8=5（级），即在温控五级870℃进行试验。比较C₁与C₂结果，若C₁优于C₂，保留第八级，舍去C₂左边部分。第三试验点： C₃＝(5+12)-8=9（级），若C₃优于C₁，舍去C₁左边部分。第四次试验点：C₄＝(8+12)-9=11（级）。若C₃优于C₄，则舍去C₄右边部分。第五次试验点： C₅＝(8+11)-9=10（级），若C₃仍优于C₅，则第9级温控为产品最佳控制温度。上述优选过程可用下图表示：

级别	1	2	3	4	5	6	7	8	9	10	11	12
温度℃	850	855	860	865	870	875	880	885	890	895	900	905
试验点					C2			C1	C3	C5	C4
比较 优劣	∵C1优于C2，舍去					∵C3优 于C1, 舍去			最 优			∵C3优 于 C4, 舍去