分布函数

设ξ为一随机变量，对任意实数x，令

称F(x)为随机变量ξ的分布函数。常被应用于测验分数统计中。

分布函数

概率论的基本概念之一。随机变量取值小于某一数值x的概率是x的函数，此函数称为随机变量的分布函数。

分布函数Distribution Function

又称“概率分布函数”。随机变量ξ取小于或等于任一实数x的概率。
它是x的函数。写作：
F (x) =P (ξ≤x)
当ξ为离散型变量时，其分布函数为：

其中，f(x_i)称为概率函数，又称频率函数，表示随机变量ζ取值x_i的概率。当ξ为连续型变量时，其分布函数为：

其中f (t)称为分布密度，又称概率分布密度，密度函数，概率密度等。对于一个极小的区间dt，随机变量ξ落入t和t+dt之间的概率接近于微分f(t)dt，后者也称概率元素。分布函数有以下性质： (1) 处于0与1之间，即0≤F (x) ≤1。(2) 单调非减，即对任意两实数x₁2，必有F (x₁₎ ≤F(x₂₎。(3)若随机变量ζ可取任何实数值，则

(4)离散型随机变量ξ的分布函数F(x)在ξ相邻两个可能数值x_i与x_i+1间保持不变； 当ξ取得下一个可能数值x_i+1时，F(x)才能跳跃性增加，故函数在x_i点是右连续。(5)连续型随机变量ξ的分布函数F(x)是连续函数，其图形y=F (x)是在直线y=0与y=1之间单调上升的连续曲线。

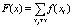
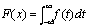
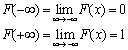
分布函数Distribution Function

设X是一个随机变量，x是任意实数，函数F(x)=P{X≤x}称为X的分布函数。对于任意实数x₁,x₂(x₁2)，有P{x₁2}=P{X≤x₂}-P{X≤x₁}=F(x₂)-F(x₁)。若已知X的分布函数，则可以得出X落在任一区间(x₁,x₂)上的概率。

分布函数distribution function

描述随机变量的统计规律性的函数。设X是一个随机变量，x是任意实数，对于任意实数x₁,x₂(x₁2)，有P{x₁2}=P{X≤x₂}-P{X≤x₁}=F(x₂)-F(x₁)，则函数 F(x)=P{X≤x}称为X的分布函数。若已知X的分布函数，就可以知道X落在任一区间(x₁,x₂)上的概率。通过分布函数能用数学分析方法来研究随机变量。如果将X看成是数轴上的随机点的坐标，分布函数F(x)在x处的函数值就表示X落在区间(-∞, x]上的概率。