函数的值域hanshu de zhiyu

即函数的因变量的取值范围.
根据已知函数的定义域及对应规律确定函数值域的基本方法是
❶直接由观察来确定.如函数y=5+，由观察可知≥0，所以函数的值域是〔5,+∞).

❷因为由函数y=f(x) 确定的反函数x=f^-1(y)的定义域就是y=f(x)的值域，所以从方程y=f(x)解出x=f^-1(y)后，便可按各种求定义域的方法来间接地求得y=f(x)的值域.如函数y=(2x-1)/(x+1)，先解得x=(y+1)/(2-y).而x=(y+1)/(2-y)的定义域是y≠2的实数，所以函数y=(2x-1)/(x+1)的值域是(-∞,2)∪(2,+∞).

❸将y=f(x)表示成y-f(x)=0，这个等式可看作含有参变数y的方程，而f(x)的值域便是使这个方程在实数域内有解的所有参变数y的值的集合.例如形如y=(a₁x²+b₁x+c₁)/(a₂x²+b₂x+c₂)的函数可变形为二次方程(a₁-a₂y)x²+(b₁-b₂y)x+(c₁-c₂y)=0，其中y是参变数.这个方程有实数根的充分必要条件是△=(b₁-b₂y)²-4(a₁-a₂y)(c₁-c₂y)≥0.利用这个不等式便可确定y的取值范围，即所求的f(x)的值域.如函数y=(x²-5x+1)/(x²-x+1)，将它变形为(1-y)x²+(y-5)x+(1-y)=0，令△=(y-5)²-4(1-y)²＝-3y²-2y+21≥0，解得-3≤y≤7/3.所以函数y=(x²-5x+1)/(x²-x+1)的值域是〔-3,7/3〕.

❹把函数y=f(x)进行换元：令t=g(x)使函数y=f(x)化为比较简明的形式y=F(t)，则函数y=F(t)(t∈D∩T，其中D为y=F(t)的定义域，T为t=g(x)的值域)的值域，就是所求函数y=f(x)的值域.如函数y=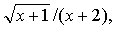

令

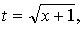
则

y=t/(t2+1).

而

y=

t/(t²+1)的定义域D为(-∞,+∞),t=的值域T=〔0,+∞)，所以D∩T=〔0,+∞)，而对任意t∈D∩T,y≥0.又当t=0时，y=0;t>0时，y=1/(t+1/t)≤1/2.所以函数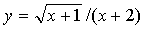的值域为〔0,1/2].