兴奋膜特性的数学模拟

兴奋膜特性的数学模拟即Hodgkin-Huxley方程。Hodgkin等(1952)根据实验中得到的gN^a和g^K变化的情况和其他实验数据，进一步对决定膜通透性改变的膜内过程作了数学模拟。他们考虑，既然gNa和gK有一个最大值(分别用N^a和^K代表)，那么在电压固定期间任一瞬间的值， 应是N^a和^K与另一随时间变化的因数的乘积，而这个因数只能取由0到1之间的值；又假定膜上与各种离子通透有关的通道只能“全或无”地取“开放”或“关闭”两种状态中的任一种，那么这个因数实际是代表了处于开放状态的某种离子通道的概率 (请注意任何随机事件的概率只能是大于0或小于1 )。Hodgkin等提出，膜内某些特殊粒子在膜电位影响下的移动，决定了某种离子通道的开放或关闭。以g^k的变化为例，根据g^k随时间变化的特点(见“电压固定实验”中的图3)，他们推测只有当四个特殊粒子在膜电场作用下移动到某一特定位置时，才能造成一个钾通道的开放；如果每个粒子到达此位置的概率为n，那么四个粒子都处于此位置的概率应为n4，就整片膜来看，亦即处于开放状态的钾通道的概率为n4。因此，在去极引起这些粒子移动的情况下，n或n4的值都由0向1变化，而gk在任一瞬间的值应是K和当时n4的值的乘积，即
g^K＝K·n4 (1a)
这里要注意的是，Hodgkin等关于四个粒子决定一个钾通道开放的假设，只是为了使g^k的理论值符合实验中得出的gk变化曲线，因为只有这种多次幂的函数，才能使gk增加时呈S形，在降低时呈指数曲线形。实际上人们早已指出，如果假定四个以上的粒子决定一个钾通道的开放，则理论上的变化曲线可以更和实际相符 (Cole,1960)。
决定钠通道状态的粒子移动与上述情况类似，但较为复杂。Hodgkin等认为，决定钠通道快速激活和随后而来的较缓慢的失活的过程，是两个独立的过程，因而由不同粒子的移动来决定。他们假定，钠通道的激活需要三个某种粒子同时处于某一位置，也就是说，如果每一粒子处于该位置的概率为m，则一个钠通道激活的概率为m³，它们的值在去极时应由0向1变化； 此外，另一种粒子的移动决定失活的出现，它在去极时移向某一位置，使钠通道不通，其概率h应是由1向0变化。这样，gNa在任一瞬间的值将由下式决定：
g^Na＝N^a·m³h (1b)
这一方程说明，只有当m3的值已相当大而h尚未接近于0时，gNa才能有一定的值，这就决定了去极化引起的钠通透性的增大只能是暂时的。换句话说，激活粒子和失活粒子的移动虽然都是膜电位的去极化引起的，但前者移动得较快，这样当m³接近于1时h尚未到0，于是钠通道激活，不久h接近于0，于是m³虽达到最大而g^Na变小，出现失活。
由式(1a)和(1b)还不能得出g^Na和g^k的变化过程，因为我们还不知道n、m和h等几个参数随时间变化的情况。Hodgkin等根据电压固定实验中得到的数据，又给出一组能满足这些实验结果的微分方程，例如对于n有
式中αn和β_n是与钾通道开放有关的粒子移动的速度常数，αn是该粒子移向使钾通道开放的位置的速度常数，βn是该粒子离开此位置的速度常数，前者在膜内电位变正时加大，而后者这时却减小。对于决定钠通道状态的粒子，则有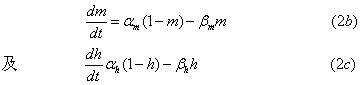
在膜内电位变正时，α_m和βh增大，β_m和α_h则减小。通过这些方程，就可算出n、m和h在任何膜电位水平和任一时间所取的值，因而可得到g^Na和g^k的变化曲线以及因此而可能出现的膜电流和跨膜电位的变化。值得提出的是，由这样的数学模型即Hodgkin-Hoxley方程计算所得的一些与膜兴奋有关的基本现象，如阈下反应、刺激阈值、强度-时间曲线、动作电位、不应期、离子通量以及膜的总阻抗的改变等，不论在变化幅度和时间经过方面，都和实验中实际测得的结果基本相符，这就说明了这些理论和数学模拟的有效性。