关系矩阵
关系矩阵guanxijuzhen
. 由0,1为元素构成的矩阵,用来表示X到Y,的二元关系R,记作MR
设X= {x1,x2,…,xn),Y= {y1,y2,…,yn),MR= (rij)m×n,
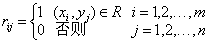
例如,X: {1,2,3,4,5},Y {a,b,c},R={ (1,a),(1,b),(4,b),(5,a),(5,c)},则
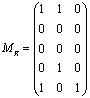
又如,A= {1,2,3,4,5},S= { (1,1),(1,2),(2,1),(3,4),(4,5),(5,1),(5,5)}.
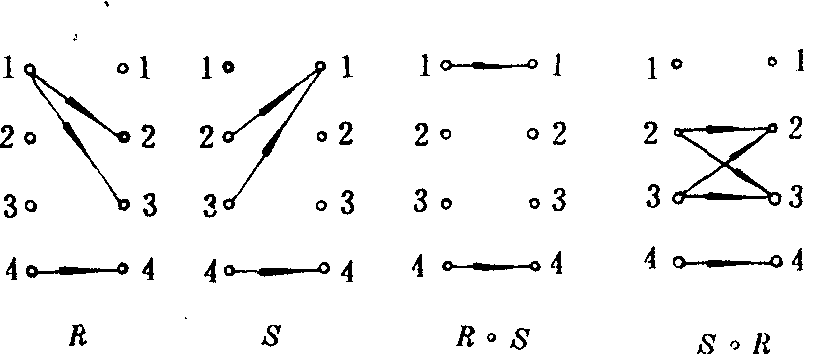
集X上的关系R,因X的元素编号 (排列)次序不同,会得到不同的关系矩阵. 但一个给定关系R的关系矩阵本质上是相同的 (即刻划的是相同点集的元素间的完全相同的关联关系).可以证明,若MR与M都是关系R的关系矩阵,则必有每行、每列都只有一个1,其余元均为0的矩阵 (称为置换方阵) P,适合
MR =P′ MP =P-1AP.
由关系R的关系矩阵MR可得逆关系R C的关系矩阵,只须将MR的行作为列、列作为行,就得到RC的关系矩阵MRC,即将肘M R的第i行第j列位置的元素换成第Aj行第i列位置的元素就可以了。
☚ 关系图 关系合成 ☛
- 老曰夫子是什么意思
- 老曲儿是什么意思
- 老更是什么意思
- 老更狂是什么意思
- 老更鹉是什么意思
- 老曼是什么意思
- 老月是什么意思
- 老有加惠是什么意思
- 老有徐来日,穷无送去时。是什么意思
- 老有所为是什么意思
- 老有所乐是什么意思
- 老有所伴是什么意思
- 老有所养是什么意思
- 老有所医是什么意思
- 老有所学是什么意思
- 老有所终是什么意思
- 老有所终,壮有所用,幼有所长,矜寡孤独废疾者皆有所养。是什么意思
- 老朋友是什么意思
- 老朋友和新朋友是什么意思
- 老朋友的感情是什么意思
- 老望天儿是什么意思
- 老朝是什么意思
- 老木是什么意思
- 老木不生秋后叶,孤灯空结夜来花。是什么意思
- 老木匠和他的儿子是什么意思
- 老木瓜是什么意思
- 老木虫是什么意思
- 老木雀是什么意思
- 老木𢙱㑈是什么意思
- 老未后儿是什么意思
- 老末是什么意思
- 老末儿是什么意思
- 老末勺儿是什么意思
- 老末拖是什么意思
- 老末独儿是什么意思
- 老本是什么意思
- 老本头是什么意思
- 老本本是什么意思
- 老本行是什么意思
- 老朱是什么意思
- 老朽是什么意思
- 老朽无用是什么意思
- 老朽无用的人或物是什么意思
- 老朽无能是什么意思
- 老朽昏庸是什么意思
- 老朽龙钟是什么意思
- 老朽(老糊涂)是什么意思
- 老杀头是什么意思
- 老杀才是什么意思
- 老杂儿是什么意思
- 老杂毛是什么意思
- 老杂毛儿是什么意思
- 老杂皮是什么意思
- 老杆是什么意思
- 老杆儿是什么意思
- 老杆子是什么意思
- 老杆橛是什么意思
- 老李是什么意思
- 老材是什么意思
- 老村是什么意思