共线向量的充要条件
共线向量的充要条件gognxian xiangliang de chongyaotiaojian
定理 两个向量a,b共线的充要条件是存在不全为零的m,n,使ma+nb=0
由此定理,可以得到两个推论:
推论1 若a,b不共线,则ma+nb=0成立的充要条件是m=n=0.
推论2.向量b与非零向量a共线的充要条件是b=ka,这里k由a,b唯一确定.
推论2表明,取定一个非零向量为基,任意一个与此向量共线的向量都可以由此向量线性表出,且表法唯一.
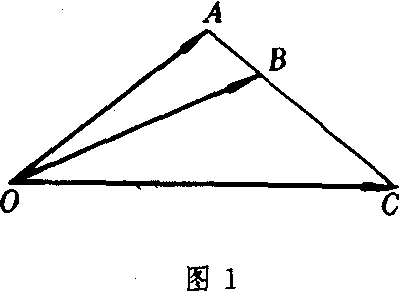
图1
把以上定理及推论用于对空间三点位置向量的讨论(图1),可以相应地得到:
定理 空间三点A,B,C共线的充要条件是存在不全为零的m,n,l,满足m+n+l=0,且使mA+nB+lC=0成立.
把向量减法
 =B-A,
=B-A, =C-B,
=C-B, =C-A引入前面的第一个定理,就可以得到这个定理.
=C-A引入前面的第一个定理,就可以得到这个定理.推论1 若三点A,B,C不共线,等式m+n+l=0和mA+nB+lC=0同时成立,充要条件是m=n=l=0.
推论2 设点A,B相异,则点C与A,B共线的充要条件是存在实数λ,μ,使C=λA+μB,且λ+μ=1,当且仅当C与A,B相异时,λ和μ都不为零.
推论2的几何意义可以从图2中得到解释:
❶C点在相异两点A,B所确定的直线上滑动,则任一时刻的C都可表成λA+μB,并且λ+μ=1.当C与A重合时,λ=1,μ=0.当C与B重合时,λ=0,μ=1.当C与A,B相异时,λ和μ都不为零.
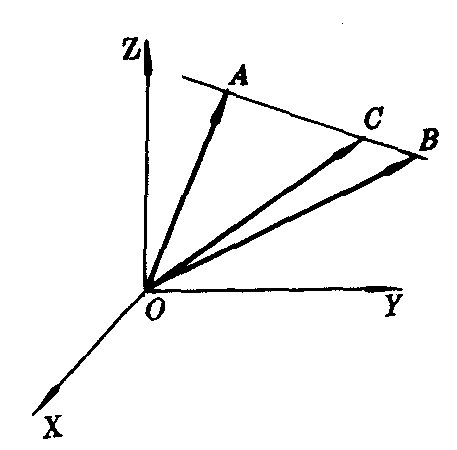
图2
❷反之,若C=λA+μB成立且λ+μ=1,则位置向量C的终点C必在位置向量A,B的终点A,B所确定的直线上.
当λ和μ连续取遍了所有满足和为1的实数值时,点C就“扫描”过了整条A,B两点确定的直线.
☚ 共线向量 两个非零向量共线的充要条件 ☛
- r2022090410000963是什么意思
- r2022090410000964是什么意思
- r2022090410000965是什么意思
- r2022090410000967是什么意思
- r2022090410000968是什么意思
- r2022090410000969是什么意思
- r2022090410000970是什么意思
- r2022090410000971是什么意思
- r2022090410000972是什么意思
- r2022090410000973是什么意思
- r2022090410000975是什么意思
- r2022090410000976是什么意思
- r2022090410000977是什么意思
- r2022090410000978是什么意思
- r2022090410000979是什么意思
- r2022090410000980是什么意思
- r2022090410000982是什么意思
- r2022090410000983是什么意思
- r2022090410000984是什么意思
- r2022090410000985是什么意思
- r2022090410000986是什么意思
- r2022090410000987是什么意思
- r2022090410000988是什么意思
- r2022090410000989是什么意思
- r2022090410000990是什么意思
- r2022090410000991是什么意思
- r2022090410000993是什么意思
- r2022090410000994是什么意思
- r2022090410000995是什么意思
- r2022090410000997是什么意思
- r2022090410000998是什么意思
- r2022090410000999是什么意思
- r2022090410001000是什么意思
- r2022090410001001是什么意思
- r2022090410001003是什么意思
- r2022090410001004是什么意思
- r2022090410001005是什么意思
- r2022090410001007是什么意思
- r2022090410001008是什么意思
- r2022090410001009是什么意思
- r2022090410001010是什么意思
- r2022090410001011是什么意思
- r2022090410001012是什么意思
- r2022090410001013是什么意思
- r2022090410001014是什么意思
- r2022090410001015是什么意思
- r2022090410001016是什么意思
- r2022090410001017是什么意思
- r2022090410001018是什么意思
- r2022090410001019是什么意思
- r2022090410001020是什么意思
- r2022090410001021是什么意思
- r2022090410001023是什么意思
- r2022090410001024是什么意思
- r2022090410001025是什么意思
- r2022090410001026是什么意思
- r2022090410001027是什么意思
- r2022090410001028是什么意思
- r2022090410001029是什么意思
- r2022090410001030是什么意思