信号的谱分析

对信号功率谱的分析称为谱分析。对随机信号作频域分析中，主要是研究其功率谱，而不是幅度的频率谱。功率谱S_x(f)正比于信号幅频函数x(f)(见“信号的频域分析”条)的平方，即S_x(f)∞|X(f)|²，它反映信号中不同频率成分的功率的相对大小。
谱分析是揭示生理信号节律的有力工具，广泛应用于各种生理信号的分析中。例如，脑电图功率谱中的频率成分随精神状态而变，睡眠时低频的δ波增加，警觉时频率较高的β波增加； 肌电图功率谱中低频成分随疲劳程度而增加。功率谱可供观察信号的频域特性，供生理、病理研究用，也可提取信号的一些频域特征(如谱峰所在的频率、峰宽、峰功率等)，组成特征集合，供进一步模式分类用。
分析随机信号的频域特征，只考虑和幅频特性平方成正比的功率谱，而不考虑相频特性，以致失去了相频信息，这是谱分析技术的先天局限性。实际上相频特性往往蕴含有有关信号细节的信息。
可以证明随机信号的自相关函数(参见“信号的相关技术”条)和功率谱是一对富氏变换对。图1是一些典型的自相关函数和功率谱的对应图象。
从物理概念上不难理解，信号的功率谱不会出现负值，而且必是实数。事实上，功率谱曲线下的面积 (如图2所示)代表着信号的总功率。这正是“功率谱”一词的由来。由一段有限长的观察值估计信号的功率谱，通常有两种途径。
❶自相关法(图3(a)):先估计信号的自相关函数(参见“信号的相关技术” 条)，再作富氏变换便得功率谱。
❷周期图法(图3(b)):先对有限长观察值作富氏变换，并取其幅图1 典型自相关函数和功率谱的对应图像频特性。然后将幅频特性平方，便得功率谱。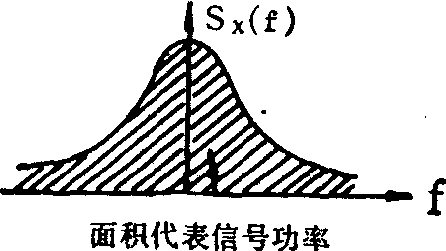

图2 信号的总功率

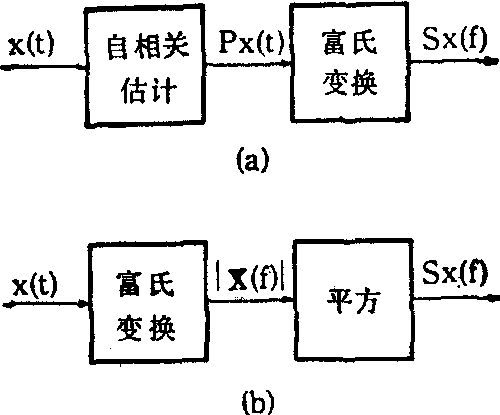
图3 估计信号功率谱的方法
(a)自相关法 (b)周期图法

互相关函数的富氏变换称为互谱。互谱有利于揭示两个信号频率成分的相似性，并能表现两信号中相应频率成分间的相位关系。