佩尔方程peier fangcheng

二次不定方程：x²-dy²＝±1 (d>0,d不是平方数).对于佩尔方程求解的问题，一般说已经解决了.华罗庚著《数论导引》(科学出版社，1957)和柯名、孙琦合著《谈谈不定方程》(上海教育出版社，1980)两书有系统而完整的论述。
关于佩尔方程x²-dy²＝1的解，有下述结果：
此不定方程有无穷多组整数解.设x²₀-dy²₀＝1，且x₀>0,y₀>0是所有满足x>0,y>0的解中使x+最小的那组解，则不定方程的全部整数解x,y可由公式x+y＝±(x₀+y₀)ⁿ,n=0,±1,±2，…表出.其中x₀,y₀叫做此不定方程的基本解.
例如，解不定方程x²-17y²＝1.先用试验法来求基本解.令y=1,2,3，…，依次计算17y²+1，直到17y²+1的值是一个平方数为止.经过计算知，使17y²+1是平方数的最小的y值是y=8.这时17y²+1=1089=33².由此可知，x₀＝33,y₀＝8就是所求的基本解.原方程的全部整数解可以表成

根据这个公式，分别令n=1,2,3可以得到这个不定方程的三组正整数解(33,8),(2177,528),(143649,34840).
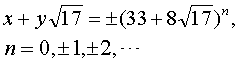
用试验法寻求基本解，有时计算十分冗长，例如不定方程x²-46y²＝1的基本解是x₀＝24335,y₀＝3588.求基本解的一般方法是，把展成简单连分数.对于d<100的情形，还有人把基本解做成表，以备查用(参看Beiler,A.H,Recreations in the theory ofnumbers,New york,1964，第254页).
关于佩尔方程x₂-dy²＝-1，则不一定有整数解.例如，x²-3y^2=-1就没有整数解.因为x²≡0,1(mod4)时，x²-3y²≡x²+y²≡0,1,2 (mod4)，而不同余于-1 (mod4)，因此它不可能有解.上例还提示，若d≡3(mod4)，则x²-dy²＝-1，一定没有整数解.但对此佩尔方程有下述一般结果，即若其有整数解，并设u²₀-dv²₀＝-1,u₀>0,v₀>0是所有x>0,y>0的解中，使x+y最小的那组解（称为这个不定方程的基本解）则此佩尔方程的全部解可以表成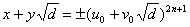

n = 0,±1 ,±2，…

并且基本解u₀,v₀与x²-dy²＝1的基本解x₀,y₀之间有下述关系：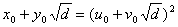

关于不定方程x²-dy²＝Q，其中d>0不是平方数，Q是非零整数，与佩尔方程有密切联系.但其解法比较复杂. 它的具体解法可以参看上述华、柯两书，还可以参看数学通报1989年第9期的“不定方程x(x-1) =D y (y-1) 的解法”.