位相weixiang

物理量按x=Acos(ω0t+ᵠ)作简谐振动时，量ω₀t+ᵠ称为谐振动的位相，又称相位或周相。用Φ表示，Φ=ω0t+ᵠ，位相是用角度表示的，故亦称之为位相角。位相虽具有角度的量纲，但它并不是指运动中的某一具体的空间角度。简谐振动中位相随时间的变化率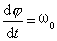，说明位相的变化是匀速的。在ᵠ随时间单调增加的过程中，描述了振动状态周期性的变化情况，位相每增加2π，振动状态就重复一次，当振动系统的振幅和圆频率一定时，振动系统任一时刻的运动状态由位相决定。t=0时的位相ᵠ叫做初位相，简称初相。初相由简谐振动系统的初位移x0、初速度v0决定。具体讲，由cosᵠ=x0/A,sinᵠ=-v₀^/ω₀A,tgᵠ=-v0/ω0x0三个方程中任选两个方程可决定ᵠ的值。由于位相增加（或减小）2nπ(n为整数)所对应的振动状态相同，所以初相通常在0～2π或-π～+π的范围中取值。同一时刻两个简谐振动的位相之差称为位相差，用ΔΦ表示。二简谐振动频率不同时，其位相差ΔΦ=(ω0₂t+ᵠ₂)-(ω0₁t+ᵠ₁)=(ω₀2-ω₀₁)t+(ᵠ2-ᵠ1)是随时间而变化的。若二谐振动的频率相同，则其位相差等于初相差，是不随时间变化的恒量。两同频率的谐振动的位相差可以反映这两个谐振动之间的步调是否一致：
❶当ΔΦ=ᵠ2-ᵠ1=±2kπ(k=0,1,2，…)时，二谐振动称为同位相（或同相），即二谐振动是同步调的。
❷当ΔΦ=ᵠ₂-ᵠ1=±(2k+1)π(k=0,1,2…)时，二谐振动称为反位相（或反相），即二谐振动步调相反。
❸当二谐振动既不同相也不反相时，ΔΦ=ᵠ2-ᵠ₁，由于不同二谐振动到达同一振动状态的时刻有相应的前后错开，这时常用某振动较另一振动超前或落后来描述二振动的步调不一致关系。这里超前或落后是指二振动到达同一振动状态的时刻谁在前面谁在后面。为了说明问题，设二谐振动为x₁₌Acos(ω0t+ᵠ1),x₂＝Acos(ω0t+ᵠ2)，如果二谐振动1和2位移相继达到正最大值的时刻为t₁和t₂，则有ω0t₁+1=ω0t₂+ᵠ2，由此可得Δ_t＝t₁-t₂＝(ᵠ2-ᵠ¹⁾/ω0。当ᵠ₂>ᵠ1，则t₂2-ᵠ₁)，或振动1比振动2的位相落后(ᵠ2-_ᵠ1)。当ᵠ₂<ᵠ₁，则t₂>t1，即振动2在振动1之后位移达到正最大值（或同一振动状态），这时称振动2比振动1落后，也可说振动2比振动1位相落后(ᵠ₁-ᵠ2)，或振动1比振动2位相超前(ᵠ1-ᵠ2)。为了简单而不致引起混乱，在比较二同频率的谐振动超前或落后时，必须在满足|ΔΦ|=|ᵠ2-ᵠ1|<π的限制条件下，再比较ᵠ2与ᵠ1的大小按上述方法来确定哪个振动超前或落后。

位相phase

又称“时相”。指同一部位在同一导联中所导出的脑波，于前后不同时间里的波的位置；或两个不同部位在同一时间（某一瞬间）里所导出的脑波的位置关系，即时间关系。