伽利略变换jialiluc bianhuan

两个作相对运动的惯性系之间的经典时空坐标变换。只适用于速度远低于光速的情况。设惯性系K静止，其时空坐标为(t、x、y、z)，另一惯性系K′的时空坐标为(t′、x′、y′、z′)。k′系的x′轴与k系的x轴重合，y′、z′轴分别与y、z轴平行。k′系以速度v沿x轴相对于k系作匀速直线运动。在k′系原点与k系原点重合的一瞬间，校准分别静止于二系的钟，使t=t′=0，于是，得到伽利略变换

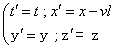
这个变换是相对性原理在经典物理学中的一种数学表达方式。它是直接从实验观测总结而来的，是速度迭加和加速度迭加的平行四边形法则的理论基础，是独立于牛顿力学三定律的一条公理。通常用三维矢量表述的牛顿力学公式在伽利略变换下是协变的，即公式的形式在此变换下不变。从上式不难看出，在伽利略变换下，尺的长度和钟的快慢都与观测者的运动状态无关，都是绝对的。实验表明，伽利略变换只适用于相对运动速度远低于光速的情况。在相对运动速度接近光速的情况下，必须用洛伦兹变换来代替它。伽利略变换只是洛伦兹变换在低速下的近似。

伽利略变换

在经典力学中，把两个彼此相对作匀速直线运动的惯性参考系中的时间和空间坐标联系起来的数学变换。