众数

杨树达《高等国文法》术语。指人称代词的复数形式。古代汉语里一般在人称代词后面加上“侪、等、曹、属、辈”等表示众数。如“吾侪、公等、我曹、尔曹、汝曹、若曹、卿曹、我属、吾属、若属、而属、尔辈”等。有的指示代词后面也可以加“属、辈、等”表示众数，如“此属、此辈、此等”等。

众数

随机变量的一种位置特征数。常用M₀表示。若随机变量X是连续型的，p(x)是它的概率密度函数，则p(x)在M₀是达到最大的值；若随机变量X是离散型的，则是使P(X=M₀)达到最大。它不一定惟一。对样本来讲，是指频数出现最多的数，在给出频数分布的情况中常用频数最大的组的组中值近似。常被应用于测验分数统计中。

众数mode

统计数列中出现次数最多的那个变量值。通常用于研究单位数较多且有明显集中趋势的总体。在单项数列的条件下，众数的确定不经计算，只要某变量值出现次数最多，该变量值即为众数。如果有几个变量值出现的次数都最多或无出现次数最多的变量值，则该数列没有众数。在组距数列的条件下，众数的计算公式为：

式中M₀为众数；L为众数所在组下限；f为众数组的次数；f₁为与众数组相邻的较小值组的次数；f₂为与众数组相邻的较大值组的次数；△为众数组组距。

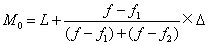
众数zhongshu

一组数据中次数出现最多的那个数，一般用符号M₀表示。可以用来表示数据的集中趋势。确定方法有两种：
用观察法找众数 当原始数据不多时，可通过观察找到众数。如在一组数据2、4、3、6、4、5、4、5中，次数出现最多的数是4，故4为众数。
在已分组的次数分布表中，可把次数最多的那一组的组中值Xc定为众数。如在“次数分布表”条的数据中，可把76～80这一组的组中值78定为众数。
用公式求众数 在次数分布表中，可用下式求众数：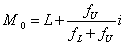

或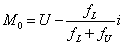

式中L——中数组的精确下限
f_L——众数组下限相邻组的次数
f_U——众数组上限相邻组的次数
i——组距
U——众数所在组的精确上限
在“次数分布表”条的数据中，L=75.5,fL=8,fU=9,i=5，故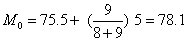

若已知算术平均数和中位数，可用下列经验公式来求众数：

M₀＝3Md-2

式中 ——算术平均数
Md——中位数
凡用公式求得的众数均为近似众数。但用此公式求得的众数要比使用次数分布表计算众数的公式准确些。

---

众数zhong shu

若随机变量X取值Mo的概率（或概率密度）是最大值，则值Mo称为随机变量X的众数，它是概率分布密度曲线上最高峰处对应的变值。
众数也就是指在样本观察值中出现最多 （即频数最大） 的数值。

众数zhong shu

又称范数、密集数、通常数等。是集中量数之一，可用来代表一组数据的集中趋势。指在一个数列中出现次数最多的数据的值。用M₀表示。众数可通过观察的方法直接得到，也可用积分方法用公式求出。前者称观察众数，后者称数理众数。众数不够稳定，易受样本变动的影响，但较少受极端数据的影响，反应不灵敏。

众数

在某一总体中出现次数最多的标志数值。变量数列中具有最多次数的变量。如用来说明工业企业工人最普遍的工资，消费者需要的内衣、鞋袜、帽子最普遍的号码等。

众数mode

指在分组资料频数中，以变量值频数最多组的组中值。

众数Mode

一组数据中出现次数最多的数值。代表数据的一般水平，不受极端数据的影响。若数据集中出现频数最高的数值为两个或两个以上，称该数据集具有双众数或多众数。

众数

被研究的事物或现象总体中，出现次数最多的变量值，即统计总体中各单位按某一标志排列后出现次数最多的标志值。众数在社会统计中通常用于总体单位充分多，而又有明显集中趋势的情况。其特点是不受少数极端变量值的影响，在掌握大量资料的情况下，可以作为变量数列水平的一个代表值，用以说明被研究总体的一般水平。确定众数要根据所掌握的资料来定。单项数列中，次数出现最多的变量值就是众数。组距数列中，众数的确定要利用公式进行计算，首先确定众数组，即出现次数最多的那个组，然后可用下列公式之一进行计算：
下限公式：

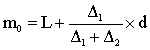
上限公式：

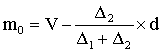
式中：m₀代表众数，L代表众数组的下限，V代表众数组的上限，△1代表众数组次数与以下一组次数之差，△₂代表众数组次数与以上一组次数之差，d代表众数组组距

众数

现象总体中出现次数最多的标志值。确定众数的方法，需要根据所掌握的资料是单项数列或组距数列来定。单项数列条件下，出现次数最多的标志值即是众数； 组距数列下，应先确定次数最多一组为众数组，然后通过一定公式进行具体计算。

众数mode

现象总体中出现次数最多的标志值。确定众数的方法，需要根据所掌握的资料是单项数列或组距数列来定。单项数列条件下，出现次数最多的标志值即是众数；组距数列下，应先确定次数最多一组为众数组，然后通过一定公式进行具体计算。

众数

集中量数之一。指一组变量值中出现次数最多的那个变量值。众数一般用M0表示。在数据分析中，众数常用来说明社会现象的一般水平。例如，为了掌握某班学生的年龄状况，就可以用最普遍的年龄为依据，假定该班80%的学生都是20岁，那么20岁这个众数就是代表他们年龄的一般水平的指标值。众数的确定，视数据资料是单项数列还是组距数列而有所不同。在单项数列中，出现次数最多的变量值就是众数；在组距数列中，则按下列公式计算众数：，式中，M0为众数，L表示M0所在组（即组距数列中频数最大的组）的下限，d表示组距，△1表示M0所在组的频数与前一组频数之差，△2表示M0所在组的频数与其后一组频数之差。众数是集中趋势的一种分析指标，一般常用来分析定类变量的资料，有时也用来分析定序、定距变量的资料。众数的特点：（一）众数是一种位置平均数，它不受各单位标志值的影响，因此作为标志值数列的平均水平有不足之处。但是，当数列中有异常标志值时，它不受两端异常值的影响，增强了作为标志值数列一般水平的代表性。（二）当分布数列没有明显的集中趋势而趋均匀分布，则无众数可言。（三）有的分布数列有多个分散的集中趋势，就应将各组次数依序双双合并，求得一个明显的集中趋势。

众数

变量数列中出现次数最多的那个变量值，也不受极端变量值的影响。在总体各变量值中代表性很强，可用来反映现象总体某一标志表现的一般水平。

众数

在某一总体中出现次数最多的标志数值。通常以M₀表示。有时一组数据中每一数值出现次数相等，就没有众数。有时出现次数最多的数值有两个或更多，则众数便不止一个。只有一个众数的数据称为单峰，有两个以上众数的称为多峰。确定众数的方法常用比例法、图解法、金氏法、组中值法、皮尔逊经验法等。

众数

总体中出现次数最多的标志数值。根据单项数列确定众数时，次数出现最多的变量值就是众数。根据组距数列确定众数时，可以利用下列公式之一进行计算：
下限公式：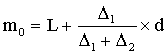
上限公式：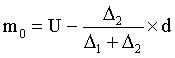
式中： m0代表众数，L代表众数组的下限，U代表众数组的上限，△1代表众数组次数与其上一组次数之差，Δ2代表众数组次数与其下一组次数之差，d代表众数组组距。众数是最普遍的、众多的标志值，可用来说明现象的一般水平。但是，众数只有在总体单位充分多，而又有明显的集中趋势时，才有意义。

众数mode

亦称“范数”。集中量数之一，简写为M0。指一系列数据中出现次数最多的一个数值。在正态分配或近似正态分配情况下，可用公式：M0=M-3(Md-M)求得。公式中Md为中数，M为平均数。对分组的组距数列，如果次数分配比较偏斜，众数所在组上下各组的次数分配相差较大时，可用下列公式计算：M0 = Lb+ fa×i/(fa+ fb)或M0 = U-fb×i/(fa+fb)。式中Lb为众数所在组的下限，fa为众数所在组下限相邻一组的次数；f b为众数所在组上限相邻一组的次数；i为组距，U为众数所在组的上限。

众数mode

在 一个数列中出现次数最多的变量值。又称密集数、范数或通常数，通常用M₀表示。它是集中量数之 一， 可用来表示一组数据的集中趋势。众数可用英国统计学家皮尔逊(Pearson, K.)的经验公式来求得：

M₀＝M-3(Md-M)

上述公式一般是在正态分配或近似正态分配的情况下使用。式中M_d为中数，M为平均数。对未经分组的单项数列，只要把变量值排列，就可以发现众数。对于分组的组距数列，如果次数分配比较偏斜，众数所在组上下各组的次数分配相差较大时， 可用下列公式计算：

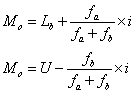
式中L_b为众数所在组的下限，fa为众数所在组下限相邻一组的次数；fb为众数所在组上限相邻一组的次数；i为组距，U为众数所在组的上限。

众数mode

亦称“范数”、“密集数”、“通常数”。集中量数的一种。在数据次数分布中出现次数最多的那个数的数值。用Mo表示。在一组数据中可能只有一个（如数据是单峰分布），也可能有好几个(如数据是双峰分布时，众数有两个；多峰分布时，众数则有多个)。

众数

亦称“范数”、“密集数”、“通常数”。集中量数的一种。用符号Mo表示。指在数据次数分布中出现次数最多的那个数的数值。