二项方程
二项方程erxiang fangcheng
形如axm+bxn=0 (m>n,a≠0)的整式方程.
设 m=k+n,则原方程可化作
xn(axk+b)=0
因此得到两个方程xn=0 axk+b=0
方程xn=0的根是n个零;因为a≠0,所以方程axk+b=0又可以化作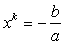
实系数二项方程
axk+b=0 (a,b∈R,a≠0)
亦可采取代数解法.通常可以通过变换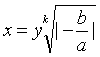
☚ 超越数 三项方程 ☛
- echoic是什么意思
- echolocation是什么意思
- echo sounding是什么意思
- echo viruses是什么意思
- echo病毒是什么意思
- eckermann,johann peter是什么意思
- eckert,john presper是什么意思
- eckhart,meister是什么意思
- eck,johann maier von是什么意思
- eclaircissement是什么意思
- eclampsia是什么意思
- eclectic是什么意思
- eclecticism是什么意思
- eclipse是什么意思
- eclipsing variable是什么意思
- ecliptic是什么意思
- eclogue是什么意思
- ecl高速、超高速双极型数字集成电路是什么意思
- eco-是什么意思
- ecologic=ecological是什么意思
- ecology是什么意思
- e-commerce是什么意思
- e-commerce是什么意思
- econometrics是什么意思
- economic(al)是什么意思
- economic and social council是什么意思
- economic growth是什么意思
- economics是什么意思
- economics of scale是什么意思
- economic systems是什么意思
- ecorche是什么意思
- ecosphere是什么意思
- ecosse nouvelle-是什么意思
- ecosse 苏格兰是什么意思
- ecosystem是什么意思
- ecotone是什么意思
- ecotope是什么意思
- ecouen 埃库昂是什么意思
- ecoutez:是什么意思
- ecrase是什么意思
- ecru是什么意思
- ecstasy是什么意思
- ect是什么意思
- ectad是什么意思
- ectasy是什么意思
- ectopia是什么意思
- ectopic pregnancy是什么意思
- ectrogeny是什么意思
- ectrosis是什么意思
- ectype是什么意思
- ectypography是什么意思
- ectypum是什么意思
- ect诊断技术是什么意思
- ect是什么意思
- ecu是什么意思
- ecuador是什么意思
- ecuador,republic of是什么意思
- ecumenical council是什么意思
- ecumenical movement是什么意思
- ecumenicity是什么意思