两个平面平行的性质定理
两个平面平行的性质定理liangge pingmian pingxing dexingzhi dingli
定理1 若两个平行平面同时和第三个平面相交,则它们的交线平行.
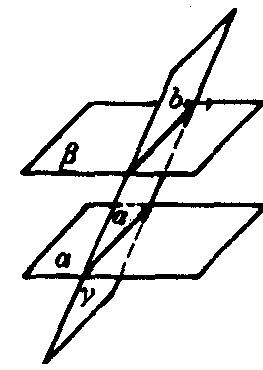
图1
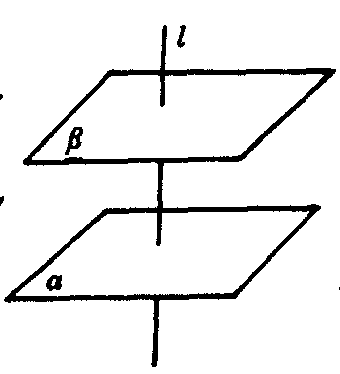
图2
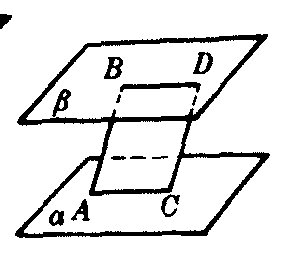
图3
如图1,若α∥β,α∩γ=a,β∩γ=b,则a∥b.
定理2 一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面.
如图2,若α∥β,l⊥a,则l⊥β.
定理3 夹在两个平行平面间的平行线段相等.
如图3,若α∥β,AB∥CD,A∈α,C∈α,B∈β,D∈β,则AB=CD.
根据两个平面平行及直线和平面平行的定义可知:两个平面平行,其中一个平面内的直线必平行于另一个平面.
此外,还有:
❶经过平面外一点有且只有一个平面和已知平面平行.
❷若一条直线和两个平行平面中的一个相交,则它和另一个也相交.
❸若一个平面和两个平行平面中的一个相交,则它和另一个也相交.
❹平行于同一个平面的两个平面平行.
❺过已知平面外一点且平行于该平面的直线,都在过已知点平行于该平面的平面内.
它们的主要应用是证明两条直线平行或直线和平面平行.
例 求证:两条直线被三个平行平面所截,所截得的对应线段成比例.
已知 直线AC和DF分别被三个平行平面α,β,γ截于A,B,C和D,E,F(图4).
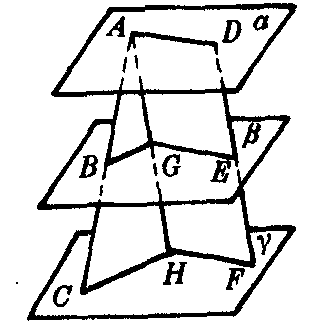
图4
| 求证 |
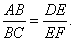
证 设过点A与DF平行的直线分别与平面β和γ交于G,H,则平面ACH∩β=BG,平面
| ACH∩γ=CH. |
| 因为β∥γ,所以BG∥CH.因此 |
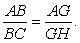 过AH与DF的平面与α,β,γ的交线分别为AD,GE,HF.因为α∥β∥γ,AH∥DF,所以AG=DE,GH=EF.
过AH与DF的平面与α,β,γ的交线分别为AD,GE,HF.因为α∥β∥γ,AH∥DF,所以AG=DE,GH=EF.| 因此 |
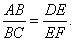
这个定理叫做平行平面截线定理.
☚ 两个平面平行的判定定理 两个平行平面的距离 ☛
- 郑惠明是什么意思
- 郑愁予是什么意思
- 郑意娘是什么意思
- 郑慎植是什么意思
- 郑慕康是什么意思
- 郑慕韩是什么意思
- 郑慧英是什么意思
- 郑懋修是什么意思
- 郑懿雅是什么意思
- 郑成是什么意思
- 郑成义是什么意思
- 郑成创是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功是什么意思
- 郑成功北伐福州之战是什么意思
- 郑成功史料选编是什么意思
- 郑成功史迹调查是什么意思
- 郑成功墓是什么意思
- 郑成功收复台湾是什么意思
- 郑成功收复台湾是什么意思
- 郑成功收复台湾是什么意思
- 郑成功收复台湾是什么意思
- 郑成功收复台湾是什么意思
- 郑成功收复台湾之战是什么意思
- 郑成功收复台湾史料选编是什么意思
- 郑成功攻南溪漳浦之战是什么意思
- 郑成功档案史料选辑是什么意思
- 郑成功满文档案史料选译是什么意思
- 郑成功纪念馆是什么意思
- 郑成周是什么意思
- 郑成法是什么意思
- 郑战成是什么意思
- 郑承典是什么意思
- 郑承振是什么意思
- 郑承瀚是什么意思
- 郑承耀是什么意思
- 郑抗北戎之战是什么意思
- 郑抗北戎之战是什么意思
- 郑拱深是什么意思
- 郑拾风是什么意思
- 郑拾风是什么意思
- 郑振乾是什么意思
- 郑振宏是什么意思
- 郑振文是什么意思
- 郑振煌是什么意思
- 郑振瑶是什么意思
- 郑振瑶是什么意思