不尽相异元素的全排列
不尽相异元素的全排列bu jin xiangyi yuansu de quan-pailie
如果n个元素里,有n1个元素相同,有n2个元素相同,………,有nr个元素相同 (n1+n2+………+nr=n),这n个元素全取的排列,叫做不尽相异的n个元素的全取的排列(简称不尽相异元素的全排列)。它的所有排列的种数是;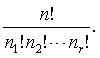
比如,现有4个相同的元素a,a,a,a和3个相同的元素b,b,b作全排列,设这7个元素的全排列种数是x. 。对每一种这样的排列,若把其中4个a分别换成a1 ,a2,a3,a4,这4个元素可以派生出P4种不同的排法;对于这P4种排法里的每一种,再把其余的3个b换成b1,b2,b3,这3个元素又可以派生出P3种排法,所以共可以有P4 · P3种不同的排法。因此,含有a1,a2,a3,a4,b1,b2,b3这7个不同元素的全排列的种数,即是含有4个a和3个b不尽相异的元素的全排列的种数x的P4·P3倍,即P7=x·P4·P3,所以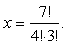
☚ 可重复的组合 多组组合 ☛
- 冯康侯是什么意思
- 冯庸是什么意思
- 冯廉是什么意思
- 冯廉直是什么意思
- 冯延已是什么意思
- 冯延已是什么意思
- 冯延巳是什么意思
- 冯延巳是什么意思
- 冯延巳是什么意思
- 冯延巳是什么意思
- 冯延登是什么意思
- 冯延铸是什么意思
- 冯廷櫆是什么意思
- 冯建吴是什么意思
- 冯建吴是什么意思
- 冯建吴是什么意思
- 冯开是什么意思
- 冯开和是什么意思
- 冯异是什么意思
- 冯异是什么意思
- 冯异是什么意思
- 冯异是什么意思
- 冯异大树是什么意思
- 冯异平定关中之战是什么意思
- 冯强橡胶厂是什么意思
- 冯彦是什么意思
- 冯征是什么意思
- 冯德培是什么意思
- 冯德培是什么意思
- 冯德培是什么意思
- 冯德培是什么意思
- 冯德尔是什么意思
- 冯德英是什么意思
- 冯德英是什么意思
- 冯德英是什么意思
- 冯德英是什么意思
- 冯德英“三花”是什么意思
- 冯德麟是什么意思
- 冯德麟是什么意思
- 冯心海是什么意思
- 冯志来是什么意思
- 冯志猛是什么意思
- 冯志珍是什么意思
- 冯志福是什么意思
- 冯志福是什么意思
- 冯志翔是什么意思
- 冯忠武是什么意思
- 冯忱妻叱李纲子墓誌是什么意思
- 冯怀珍是什么意思
- 冯思义是什么意思
- 冯思温是什么意思
- 冯思炘是什么意思
- 冯恭钊是什么意思
- 冯惟敏是什么意思
- 冯惟敏是什么意思
- 冯惟敏是什么意思
- 冯惟敏是什么意思
- 冯惟讷是什么意思
- 冯愉态是什么意思
- 冯慧妍是什么意思