三面角的性质
三面角的性质sanmianjiao de xingzhi
❶三面角的任何一个面角小于其他两个面角的和,而大于其他两个面角的差.
❷三面角的所有面角之和小于360°.
❸三面角的所有二面角之和大于180°,而小于540°.
如图1,若三面角S-A1B1C1的三个二面角的大小分别为α,β,γ,则180°<α+β+γ<540°.
证 在三面角内任取一点P.过P点向平面A1SB1,B1SC1,C1SA1分别作垂线PF,PD,PE,垂足分别为F,D,E.过PD,PE作平面CDPE,交SC1于C,则平面CDPE⊥平面B1SC1,平面CDPE⊥平面C1SA1.因此SC1⊥平面CDPE.所以∠DCE为二面角A1-SC1-B1的平面角,设为r.在四边形CDPE中,因为∠PDC=∠PEC=90°,所以∠DPE+r=180°.用同样的方法可以作出二面角B1-SA1-C1和A1-SB1-C1的平面角∠EAF和∠DBF,设它们分别为α,β,则有∠EPF+α=180°和∠DPF+β=180°. 于是有∠DPE+γ+∠EPF+α+∠DPF+β=540°. 因此α+β+γ=540°-(∠EPF+∠DPF+∠DPE).但由于0°<∠EPF+∠DPF+∠DPE<360°,所以540°-360°<α+β+γ<540°,即180°<α+β+γ<540°.
❹设三面角的三个面角为α,β,γ,它们所对的
| 二面角分别为A, B, C, 则有 |
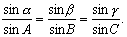
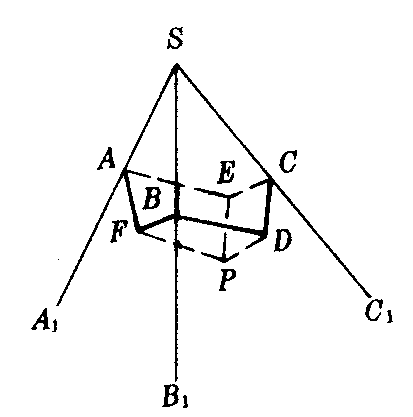
图1
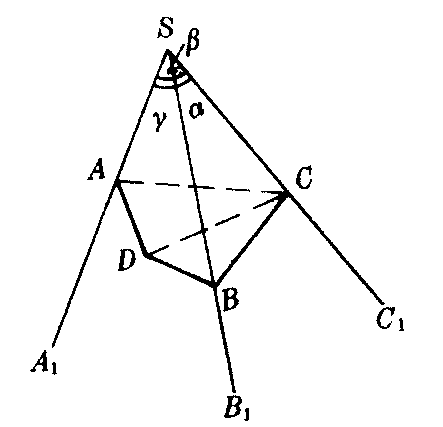
图2
证 如图2,在棱SC1上截取SC=1,过点C作平面A1SB1的垂线CD,垂足为D.过点C在平面A1SC1内作CA⊥SA1于A,则DA⊥SA1.所以∠DAC是二面角B1-SA1-C1的平面角.同理,过C在平面B1SC1内作CB⊥SB1于B,则∠CBD是二面角A1-SB1-C1的平面角.在Rt△SCB中,CB=1·sinα=sinα.在Rt△SAC中,AC=1·sinβ=sinB.在Rt△CBD中,CD=CB·sinB=sinα·sinβ.在Rt△CAD中,CD=AC·sinA=sinβ·sinA. 因此sinα·sinB=
| sinβ·sinA, |
| 即 |
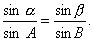
| 同理可证 |
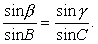
| 所以 |
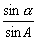
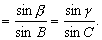
上面的公式叫做三面角的正弦公式.
❺设三面角的三个面角为α,β,γ,它们所对的二面角分别为A,B,C,则有
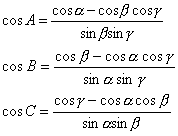
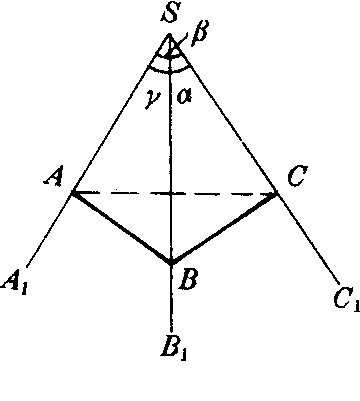
图3
证 如图3,在棱SA1上任取一点A.过点A在平面SA1B1内作SA1的垂线交SB1于B,过点A在平面SA1C1内作SA1的垂线交SC1于C,连结BC,在△SBC中,由余弦定理有BC2=SB2+SC2-2SB·SCcosα.在△ABC中,有
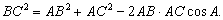
| 因为 |
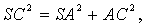
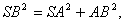
| 所以 |
| SB·SCcosα=AB·ACcosA+SA2 |
| 即 |
| AB·ACcosA=SB·SCcosα-SA2. |
| 因此 |
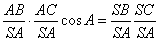
| cosα-1, |
| 于是有 |
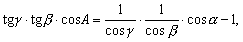
| 所以 |
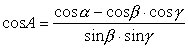
| 同理可证 |
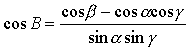
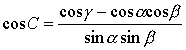
上面的公式叫做三面角的余弦公式.
☚ 直三面角 多面角的性质 ☛
- 大酒大肉是什么意思
- 大醇小疵是什么意思
- 大野是什么意思
- 大量是什么意思
- 大量生产是什么意思
- 大金是什么意思
- 大钞是什么意思
- 大钱是什么意思
- 大锅饭是什么意思
- 大错是什么意思
- 大错特错是什么意思
- 大锣大鼓是什么意思
- 大锤是什么意思
- 大门是什么意思
- 大门不出,二门不迈是什么意思
- 大队是什么意思
- 大阪是什么意思
- 大陆是什么意思
- 大陆坡是什么意思
- 大陆岛是什么意思
- 大陆性气候是什么意思
- 大陆架是什么意思
- 大陆桥是什么意思
- 大陆漂移是什么意思
- 大限是什么意思
- 大限临头是什么意思
- 大院是什么意思
- 大难是什么意思
- 大难不死是什么意思
- 大难不死,必有后福是什么意思
- 大难临头是什么意思
- 大雁是什么意思
- 大雄是什么意思
- 大雄宝殿是什么意思
- 大雅是什么意思
- 大雅之堂是什么意思
- 大集是什么意思
- 大集体是什么意思
- 大雨是什么意思
- 大雨倾盆是什么意思
- 大雨如注是什么意思
- 大雨滂沱是什么意思
- 大雪是什么意思
- 大雪山是什么意思
- 大雪纷飞是什么意思
- 大雷雨是什么意思
- 大面儿是什么意思
- 大革命是什么意思
- 大顺是什么意思
- 大题是什么意思
- 大题小作是什么意思
- 大额是什么意思
- 大风是什么意思
- 大风大浪是什么意思
- 大餐是什么意思
- 大饭店是什么意思
- 大饱眼福是什么意思
- 大饼是什么意思
- 大马哈鱼是什么意思
- 大马士革是什么意思