万能置换法解三角方程wanneng zhihuanfa jie sanjiaofangcheng

解三角方程的一种方法.其特点是对方程中的所有三角函数施用万能代换，使三角方程转化为代数方程，以便用代数方法来求解.

例 解方程

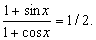
解 设

tgx/2=t,

则

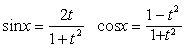
代入原方程并化简，得关

于t的整式方程t²+2t=0
若 tg(x/2)=t=0，则x=2kπ
若 tg(x/2)=t=-2，则x=2(kπ-arctg2)
故x=2kπ,x=2(kπ-arctg2)(k∈Z)
经检验x=(2k+1)π不是原方程的根，所以原方程没有遗根.
应用万能置换法，不但可能使原方程遗根，有时还会引进高次方程，所以若有别的方法，就不用万能置换法.