DW检验

---

关于随机变量一阶线性序列相关(自相关)的一种检验。

它是由德宾(Durbin)和瓦森(Watson)提出的。随机变量e的一阶线性自相关可写为：

e_t=pe_t－t+ε_t

式中，p为自相关系数，εt系均值为0、无自相关的随机变量。DW检验是关于上式中的p的某一假设的检验。其检验指标是：

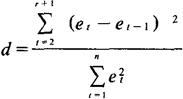
d的值介于0与4之间。

对于假设p=0，德宾和瓦森给出了0．5和0．1显著水准的d的上限d_u和下限d_I。如果实际观察到的d^*小于d_L或大于4－d_L，则拒绝原假设。如果d^*界于d_u和4－d_u之间，则接受原假设。如果d_L＜d^*＜d_u或者4－d_u＜d^*＜4－d₁，则无结论。