17世纪数学shiqi shi ji shuxue

17世纪是数学史上继希腊时代之后的辉煌的世纪.数学在这一百年间从具体成果的取得，旧分支的扩展，新分支的建立到一般数学思想与方法的飞跃，都是以往任何时代所无法比拟的.
这一世纪的前三分之一继续着上一世纪的研究，1614年，纳贝尔公布了他发明的对数，1620年，E.冈特发明了对数刻度尺，并由W·奥特雷德在大约1622年发展为对数计算尺，1631年，T·哈里奥特以及W·奥特雷德的代数著作于同年出版，使16世纪由韦达初步建立的代数符号体系得到进一步的发展.这些工作以及文艺复兴运动带来的思想解放、科学发展、技术进步以及科学方法的建立，促成了近代数学时期的到来.
大约在1630年，费尔马写成了他的小册子《平面与立体轨迹引论》，虽然直到1679年才得以出版，但其中的思想与方法已在同时代人中产生了影响.与此同时，笛卡尔也在酝酿着他的突破，1637年，他的《几何学》作为其科学哲学巨著《方法论》的附录出版，成为第一部正式发表的解析几何著作.费尔马与笛卡尔熟知古希腊数学家在圆锥曲线研究方面的成就，都以此为基础展开自己的工作，并且都抓住了这样一些关键思想：把几何问题与代数问题综合起来考虑，通过引入坐标建立平面上的点与有序数对的一一对应，通过引入变量使曲线的问题化为方程的问题，通过研究方程的性质确定曲线的性质.因而，他们都是解析几何的独立创立者，他们的工作，标志着数学思想中一次伟大变革的开始，并为微积分的创立做了准备.
微积分是17世纪最辉煌的数学创造，同时也是两千年来人类心智奋斗的结晶.这种奋斗从希腊时代的第一次数学危机，特别是芝诺悖论的提出就开始了.历史上与之相关的重要工作包括欧多克斯的穷竭法，阿基米德求切线、面积与体积的方法，中世纪后期的形态幅度研究，以及17世纪早期的不可分量的研究.由于对变速运动的规律，曲线切线、函数极值、物体重心和引力以及与曲线、曲面有关的各种度量问题的研究，到17世纪中期已经积累了大量的具体成果和方法，而从众多零散成果中确立微积分的基本概念、普遍方法和一般形式的历史使命就落到了牛顿与莱布尼兹身上.
牛顿称自己的微积分为“流数术”，大致经历了四个发展时期：
❶初建于1664年秋至1667年初，以被称为《1666年10月流数简论》的一篇总结性论文为代表.这是历史上第一篇系统的微积分文献，其中已经明显地建立了微积分的基本定理.
❷对几何不可分量观点的动摇，以1669年的《运用无限多项方程的分析学》为代表.
❸成熟于1671年，以《流数法与无穷级数》为代表.
❹首末比法的提出与改进是在17世纪70年代中至90年代初，以《曲线求积术》(初稿写于1691年)为代表，其基本思想贯穿于他的划时代巨著《自然哲学的数学原理》(1687)中.
莱布尼兹1673年左右接触到了微积分学的实质性问题，注意到切线问题与求积问题的互逆关系，即微积分基本定理，并建立了特征三角形.与牛顿相比，莱布尼兹更偏重于发展微积分的形式化算法和建立一套简洁、明确而有效的符号.莱布尼兹的工作独立于牛顿，大约完成于1675年，并于1684年先于牛顿发表了第一篇微积分论文.
在解析几何，微积分诞生的同时，数学的其他分支也在蓬勃发展.1639年，G·笛沙格发表论文《试论锥面截一平面所得结果的初稿》，由于把无穷远元素引入几何学，为空间射影概念奠定了基础，从而得到了射影几何中的一些基本命题，其中最重要的是“笛沙格定理”.通过研究笛沙格的著作，年仅16岁的帕斯卡得出了圆锥曲线的射影几何中的一些新的定理，于1640年发表了题为《略论圆锥曲线》一文，其中包括了著名的帕斯卡定理.
1637年，笛卡尔在他的《几何学》中首次给出了关于高次代数方程正根与负根的笛卡尔符号法则.
1653年，帕斯卡写成《论算术三角形》一书(1665)年出版)，给出了推求二项式系数的一般方法以及许多关于二项式系数的命题，并且对最基本的组合模型——n件中一次取r件的组合数给出了基本关系，相当于

还给出了数学归纳法的最早陈述.由于帕斯卡的卓越工作，虽然甚至在欧洲他也不是最早的研究者，但二项式系数表仍被称为帕斯卡三角.1665年，牛顿给出了一般的二项式定理，1671年他又给出了求方程实根近似值的牛顿法.1693年，莱布尼兹在考虑关于齐次线性方程组的形成创立了行列式理论.
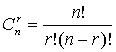
17世纪的数论与费尔马的名字联系在一起，最著名的结果有费尔马小定理：每个奇素数可用且仅可用一种方式表为两个平方数的差，形如4n+1的素数可以表为两个平方数的和；边长为整数的直角三角形，其面积不能是一个平方数.费尔马通常只是给出命题却很少详细证明，其证明大多由欧拉和拉格朗日在18世纪给出.但最著名的费尔马大定理xⁿ+yⁿ＝zⁿ(n≥3)不存在非零整数解却至今未获证明.为了解决这一难题，300多年来人们付出了无数心血，从而产生了许多新概念，新方法和新结果，推动了数论乃至整个数学的进步，因此被希尔伯特称之为“下金蛋的母鸡”.此外，M·莫森尼研究了形如2^p-1 (p为素数)的素数（现称为莫森素数），使数学家们对完全数的认识得以推进，在他之前，卡塔尔迪已对此做了不少努力.
1654年，帕斯卡的朋友梅雷向他询问了早在15世纪已出现的赌博中断问题：“两个赌徒相约赌若干局谁先胜s局就赢得全部赌金，但是当一个赌徒胜a局(a数学期望”这一重要的概念.
在17世纪，由于使用文字系数而使证明有了一种尺度，代数已上升为一门科学，其方法和理论都大大扩展了；数论因费尔马的工作获得了进展；此外，射影几何与概率论的开端，解析几何的创立，函数概念的明确提出；尤其重要的——微积分的诞生，而使数学从根本上改变了面貌.特别是，由于解析几何与微积分的创造，代数与几何的地位发生了与古希腊时不同的逆转，其追求方法和成果的普遍性已成为17世纪和以后几个世纪数学的特征.数学期望”这一重要的概念.>

17世纪数学17shiji shuxue

17世纪是数学史上的辉煌世纪。这100年间数学的进步，从旧分支的扩展，新分支的建立到一般数学思想与方法的飞跃。都是前所未有的。
这一世纪的前三分之一继续着上一世纪的研究，这些工作以及文艺复兴运动以来科学技术的发展与思想方法的进步， 促成了近代数学时期的到来。
17世纪30年代， 费尔马与笛卡尔分别以古希腊的圆锥曲线理论为基础展开研究， 通过引入坐标与变量概念建立了几何中的曲线与代数中的方程之间的内在联系， 创立了解析几何学。费尔马的著作完成于1630年左右，虽然到1679年才得以出版，但其思想与方法已在同时代人中产生了影响，笛卡尔的《几何学》作为他的巨著《方法论》的附录，于1637年正式出版。他们的工作标志着数学史上一场伟大变革的开始。并为微积分的创立作了准备。
微积分是17世纪最辉煌的数学创造，也是自希腊时代以来数学中一系列重要创造的继续和发展， 它们包括欧多克斯的穷竭法，阿基米德求切线、面积、体积的方法，中世纪后期的形态幅度研究，以及17世纪早期的不可分量研究。尤其是自文艺复兴后期以来，由于科学技术中各种实际问题的推动， 对变速运动规律的研究，对曲线切线、函数极值、物体重心和引力的研究，以及对曲线、曲面各种度量问题的研究，到17世纪中期已经积累了大量具体成果和方法。牛顿和莱布尼茨的历史功绩在于从众多零散成果中确立了微积分的基本概念、普遍方法和一般形式，使之最终成为一门完整而统一的数学分支。
牛顿称自己的微积分为“流数术”。初创于1664年秋至1667年初。1666年10月， 他完成了第一篇系统的微积分论文，此后在将近40年的时间里不断改进和发展了这一理论， 写成了不少论著， 但大部分发表很晚， 最早出版的体现微积分思想与方法的著作是他的划时代巨著《自然哲学的数学原理》(1687)。莱布尼茨于1673年左右独立于牛顿接触到微积分的实质性问题，大约在1675年完成了创建微积分的工作。与牛顿的工作相比， 他更注重于发展微积分的形式化算法和建立一套简洁、明确而有效的符号。他于1684年先于牛顿发表了第一篇微积分论文。
1639年，笛沙格(Desargues,G.)在一篇论文中把无穷远元素引入几何学， 得到射影几何中的一些基本命题，特别是重要的“笛沙格定理”。通过研究笛沙格的著作，帕斯卡得到射影几何中另一些重要定理，尤其是著名的帕斯卡定理， 并于1640年发表了论文。
17世纪，由于使用字母系数而使证明有了一种尺度，代数学已上升为一门科学，方法和理论都大大扩展了。1637年， 笛卡尔在《几何学》中给出了关于高次方程正根与负根个数的笛卡尔符号法则。1653年，帕斯卡在《论算术三角形》一书 (1665年出版) 中深入地讨论了二项式系数和基本的组合关系， 并给出了数学归纳法的最早陈述。1665年，牛顿给出了有理指数的二项式定理，1671年他又给出了求方程实根近似值的牛顿法。1693年， 莱布尼茨创立了行列式理论。
17世纪的数论主要是在费尔马的推动下进步的，他给出了关于素数、完全数、亲和数、不定方程等方面的许多重要结果，但通常只是给出命题却很少证明，其证明大多由欧拉和拉格朗日在18世纪给出，但最著名的费尔马大定理（参见该条）至今仍未获证明。此外，默森尼研究了形如2^p-1(p为素数)的素数(参见“默森尼数”)，笛卡尔给出了一条探索亲和数的规则，莱布尼茨得到了后人所说的用于素数检验的威尔逊定理。
1654年，帕斯卡与费尔马在通信中讨论了“赌博中断问题”，从而共同创立了概率论。在此基础上，1657年惠更斯发表了概率论的第一篇正式论文—— 《论赌博中的推理》，其中首次引入了 “数学期望”这一重要概念。
这一时期计算技术的一个十分引人注目的进步是原始计算机的发明。1623年， 德国科学家席卡德(Schickhard, W.) 制造了第一台机械计算机的模型。1642年，帕斯卡制成了第一台可供实用的计算加减法的机械， 1671年，莱布尼茨制成了可进行加减乘除运算的计算机。这些工作标志着计算已由手工时代进入机械时代， 并成为后世电子计算机的源头。
17世纪的数学不仅由于解析几何与微积分的创立而成为近代数学的开端，它在数学成果、方法与思想各方面的丰富创造也对后世数学的发展产生了极为深远的影响。