连续型随机变量的概率分布

---

概率密度函数 设随机变量X的分布函数为F(x)，且有非负值函数f(x)，如果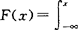f(t)dt，则称f(x)为X的概率密度函数，简称为密度函数．

概率密度函数的性质

(1)f(x)≥0．

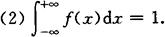
(3)F(x)是连续函数．

(4)对任何点x，恒有P｛X=x｝=0．由此可想到，概率为0的事件，不一定是不可能事件．

(5)在f(x)的连续点，F(x)可导，且有F′(x)=f(x)．

对任何值a，b，都有

由此可看出，对连续型随机变量，个别点(甚至有限个点)的存在与否，不影响区间上的概率值．

几个重要的连续型随机变量的概率分布

1．均匀分布X～U(a，b)

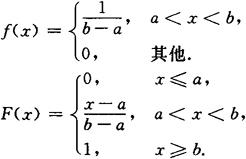
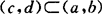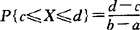性质 若，则有(几何概率)．

2．指数分布X～E(λ)

性质 若X～E(λ)，则对任何正数x，x₀，必有P｛X＞x+x₀|X＞x₀｝=P｛X＞x｝．

3．正态分布X～N(μ，σ²)

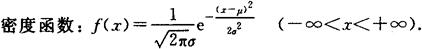
(1)x=μ是f(x)图形的对称中心，μ的大小影响图形的位置；

(2)σ的大小影响图形的形象，σ大，图形“矮胖”，σ小，图形“瘦高”．

标准正态分布：X～N(0，1)，μ=0，σ=1．

重要性质：

(1)Φ(x)+Φ(－x)=1．

(2)Φ(x)－Φ(－x)=2Φ(x)－1．

(3)若X～N(μ，σ²)，则．称X^*为标准化随机变量．

由X得到X^*这种做法叫正态分布的标准化步骤．解决正态分布的计算问题最重要的，首先要考虑的就是对X进行标准化．

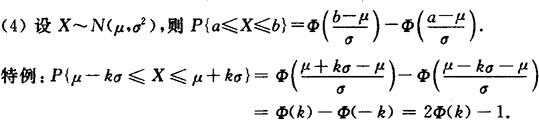
它的等价形式为

P｛|X－μ|≤kσ｝=2Φ(k)－1．

此概率值与μ，σ的大小无关，只与k的数值有关．由此得出下面几个重要数字：

P｛|X－μ|≤σ｝=2Φ(1)－1≈2×0．8413－1=0．6826．

P｛|X－μ|≤2σ｝=2Φ(2)－1≈2×0．9772－1=0．9544．

P｛|X－μ|≤3σ｝=2Φ(3)－1≈2×0．9987－1=0．9974．

最后一个数值说明X落在区间［μ－3σ，μ+3σ］上的概率达到99．74%．它表明X落在上述区间之外的概率已不足0．3%．可以认为X几乎不在该区间之外取值．这个结果在专业上通常称为“3σ规则”．

4．Γ分布

设随机变量X，若X的概率密度函数为

则称X服从参数为λ，r的伽马分布，简称为Γ分布，记为X～G(λ，r)，其中Γ(r)为Γ函数，定义为

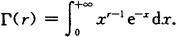
Γ函数有下面的性质：

Γ(r+1)=rΓ(r)，

并有

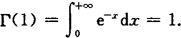
当r=1时，有

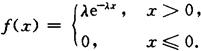
这时，X服从参数为λ的指数分布．说明指数分布是伽马分布的一个特例．X～E(λ)，即X～G(λ，1)．