矩阵运算

---

1．相等、加减、数乘

相等：两同阶矩阵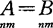指a_ij=b_ij

加减：若A、B同阶，则

A±B=(a_ij±b_ii) (2．3－2)

数乘：若α为一个数，则

αA=(αa_ij) (2．3－3)

2．乘法

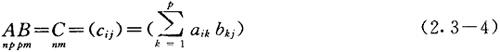
即C的i行j列元素c_ij，为A的i行各元素与B的j列各对应元素乘积之和。

3．求逆

对于方阵A，若

AB=BA=I

则称B为A的逆，记为B=A^－1，A有逆的充要条件是A的行列式非零(即｜A｜≠0，亦称A非异)。逆可由下式计算

式中A_ij为A中a_ij代数余子式(划去A中i行j列，由余下的(n－1)(n－1)阶方阵的行列式乘(－1)^i+j而得)

4．运算律

(1)A+B=B+A，(A+B)+C=A+(B+C)=A+B+C

(2)α(A+B)=αA+αB

(3)(AB)C=A(BC)=ABC

(4)(A+B)C=AC+BC，A(B+C)=AB+AC

(5)AI=IA=A，AO=OA=O

(6)(AB)′=B′A′，(A+B)′=A′+B′，(A′)′=A

(7)(A′)^－1=(A^－1)，(AB)^－1=B^－1A^－₁，(A^－1)^－1=A

(8)｜A^－1｜=｜A｜^－1

〔例2．3－1〕

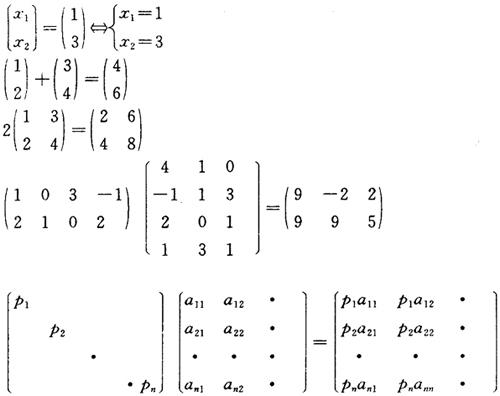
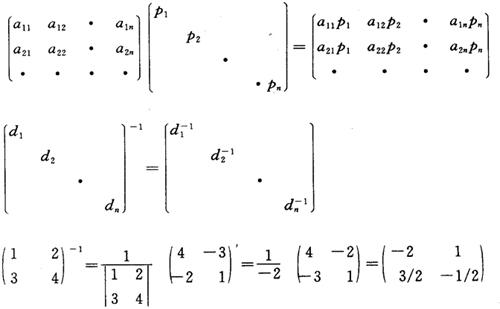
〔例2．3－2〕 建立矩阵线性方程

在计量工作中，经常有多个待求量，它们可以形成函数关系，通过测量这些量的函数，确定待求量。经常遇到的是线性函数，或可以化为线性函数，即待求的x₁，·，x_n间的线性函数，形成线性方程

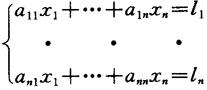
由测得的已知数l₁，·，l_n，求x₁，·，x_n时，首先将系数a_ij，已知数l_i，待求数x_i用矩阵表示为：

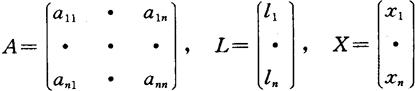
由矩阵的乘法与相等运算，可知上述线性方程等价于

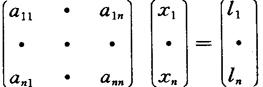
即AX=L，两端乘逆A^－1，由于AA^－1=I，IX=X，故得解

X=A^－1L

〔例2．3－3〕解线性方程

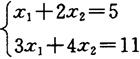
这一方程用矩阵可以写为

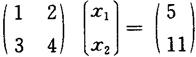
故解为

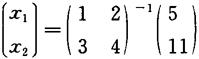
因

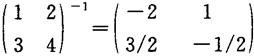
故得解

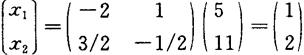
即：x₁=1，x₂=2。

当n很大时，用矩阵表示线性方程并求解，既简单又方便。

【参考文献】：

［1］王立吉，计量学基础，中国计量出版社，1988。

［2］BIPM、IEC、IFCC，IUPAC，IUPAP，OIML，Guide to the Expression of Uncertainty in Measurement， ISO，1993．

［3］刘智敏，不确定度原理，中国计量出版社，1993。

［4］刘智敏，误差分布论，原子能出版社，1988。

［5］刘智敏，误差与数据处理，原子能出版社，1983。

［6］Liu Zhimin(刘智敏)，Measurement Uncertainty and Its Correlation Combination，Proceeding of ISEM， 1993．

［7］国家计量总局量值传递处编，计量技术考核纲要，计量出版社，1981。

［8］国家技术监督局审定，刘智敏等编审，全国计量检定人员考核统一试题集第六分册三，误差及数据处理，陕西科学技术出版社，1990。