矩阵及其基本运算

---

矩阵 由m×n个数a_ij(i=1，2，…，m；j=1，2，…，n)排成的m行，n列的数表

称为m行n列矩阵，简称m×n矩阵．这m×n个数称为矩阵A的元素，a_ij是矩阵A的第i行第j列的元素．元素是实数时，矩阵称为实矩阵；元素是复数时称为复矩阵．

(1)式也简记作

A=(a_ij)_m×n，A=(a_ij)或A_m×n．

n阶方阵 当m=n时，A称为n阶方阵．

行矩阵 只有一行的矩阵

A=(a₁，a₂，…，a_n)

称为行矩阵．

列矩阵 只有一列的矩阵

称为列矩阵．

零矩阵 元素全部为0的矩阵称为零矩阵．记作0．

负矩阵 设A=(a_ij)_m×n，则A=(－a_ij)称为A的负矩阵，记作－A．

同型矩阵 两个矩阵的行数、列数对应相等时，称为同型矩阵．

两个矩阵相等 矩阵A，B相等要求A和B是同型矩阵，且对应元素相等，即，B=(b_ij)_m×n，且a_ij=b_ij，

i=1，2，…，m；j=1，2，…，n．

矩阵的线性运算

1．加法

设A=(a_ij)_m×n，B=(b_ij)_m×n，矩阵A与B的和记作A+B，定义为对应元素之和，即

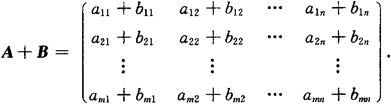
注 只有两个同型矩阵才能相加．

2．数与矩阵的乘法

设k是一个数，A是一个m×n矩阵，则数k和矩阵A的乘积kA或Ak定义为数k乘矩阵的每个元素，即

线性运算的性质 矩阵的加法和数乘，称为矩阵的线性运算，且满足

(1)加法交换律：A+B=B+A．

(2)加法结合律：(A+B)+C=A+(B+C)．

(3)存在零矩阵0，使得A+0=A．

(4)存在负矩阵－A，使得A+(－A)=0．

(5)1A=A．

(6)分配律：k(A+B)=kA+kB．

(7)分配律：(k+l)A=kA+lA．

(8)数与矩阵乘法的结合律：k(lA)=(kl)A=l(kA)．

3．矩阵的乘法

设A=(a_ij)是m×s矩阵，B=(b_ij)是s×n矩阵，则定义矩阵A和B可以相乘，且乘积是一个m×n矩阵C=(c_ij)，其中，i=1，2，…，m；j=1，2，…，n．且记作

A_m×sB_s×n=C_m×n．

注 只有左边矩阵的列数等于右边矩阵的行数时，两个矩阵才能相乘．

矩阵乘法的运算性质：

(1)结合律：(AB)C=A(BC)．

(2)分配律：A(B+C)=AB+AC，(B+C)A=BA+CA．

(3)数与矩阵乘积的结合律：(kA)B=A(kB)=k(AB)．

注 矩阵乘法不满足交换律，即在一般情况下，

AB≠BA，

故应区分左乘与右乘．从而在一般情况下，也没有消去律，即若

AB=AC，

一般不能得出B=C的结论．

4．方阵的幂

A是n阶方阵，m个A连乘，称为A的m次幂，记作A^m，即

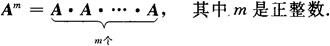
规定A⁰=E(单位阵)．

方阵的幂的运算性质：

(1)A^k·A^l=A^k+l；

(2)(A^k)^l=A^kl．

其中k，l是非负整数．

注 矩阵乘法没有交换律，故

(A+B)²=A²+AB+BA+B²≠A²+2AB+B²．

(A－B)²=A²－BA－AB+B²≠A²－2AB+B²．

(A－B)(A+B)=A²－BA+AB－B²≠A²－B²．

5．矩阵的转置

将矩阵A_m×n的行列互换得到一个n×m矩阵，称为A的转置阵，记作A^T，即设

则

矩阵转置的运算性质：

(1)(A^T)^T=A．

(2)(kA)^T=kA^T．

(3)(A+B)^T=A^T+B^T．

(4)(AB)^T=B^TA^T．