渠道横断面
(-)横断面形式
渠道横断面形式有梯形、矩形、多边形、U形及复式断面,见图2-7-1。
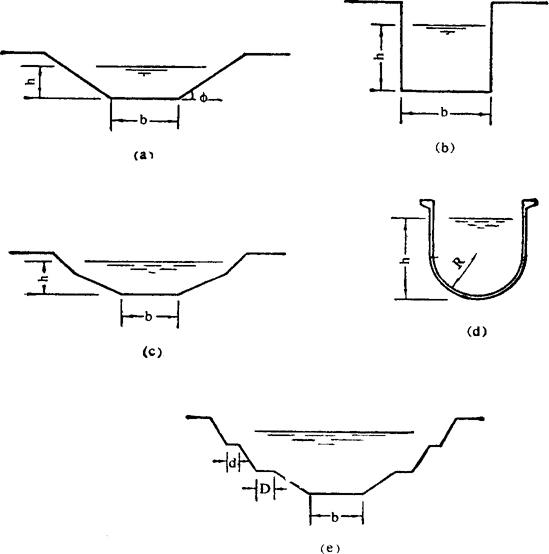
图2-7-1 渠道断面形式示意图
a-梯形断面 b-矩形断面 c-多边形断面 d-U形断面 e-复式断面
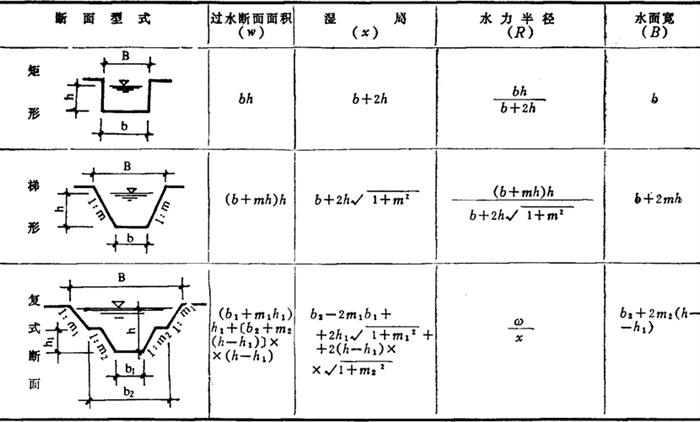
矩形、梯形及复式断面的水力要素见表2-7-1。
表2-7-1 渠道断面水力要素计算公式表
(二)横断面选择
渠道断面可分为宽浅与窄深两类。宽浅渠道断面的水流比较稳定,水深变幅小,不易淤积或冲刷,在适当的地形条件下,挖、填方量可以平衡;但在相同水位下所需的过水断面较大。盐田输水渠道,一般多采用这种断面。
1.梯形渠道断面的计算
(1)渠道断面水力计算通过渠道断面的流量可利用明渠均匀流的谢才公式计算:

根据流量定义:

式中 Q——通过渠道的流量(m3/s)
ω——过水断面面积(m2)
i——渠道底坡
R——水力半径(m),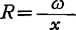
x——湿周(m)
C——谢才系数,通常采用曼宁公式(2-7-3)和巴甫洛夫斯基公式(2-7-4)进行计算
曼宁公式:

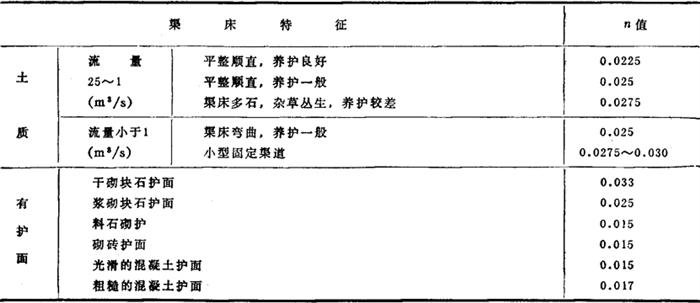
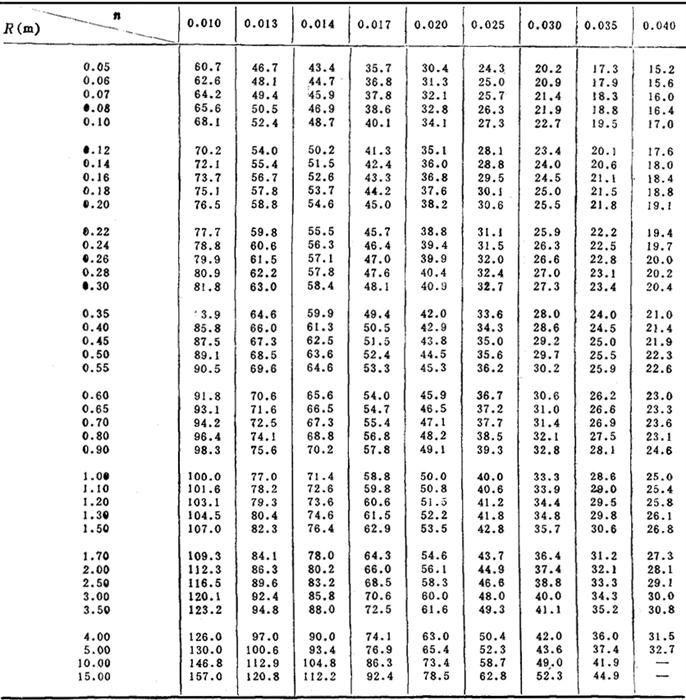
式中 n——边壁糙率,根据渠床土质及渠床砌护材料而异,见表2-7-2
表2-7-2 渠道糙率n值
曼宁公式的C值可由表2-7-3查得。
表2-7-3 谢才系数C值表
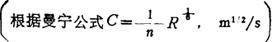
巴甫洛夫斯基公式:

式中 y——指数,y=2.5 -0.13-0.75
-0.13-0.75 (
(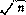 -0.1)
-0.1)
巴甫洛夫斯基公式,适用于0.1m≤R≤3.0m时的明渠。
巴甫洛夫斯基并提出下列的简便计算公式,求取C值的近似值:
当R<1.0m时 y=1.5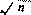
当R>1.0m时 y=1.3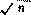
按巴甫洛夫斯基公式,对不同的n及R,其系数C值见表2-7-4。
表2-7-4 谢才系数C值表
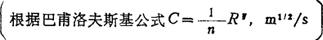

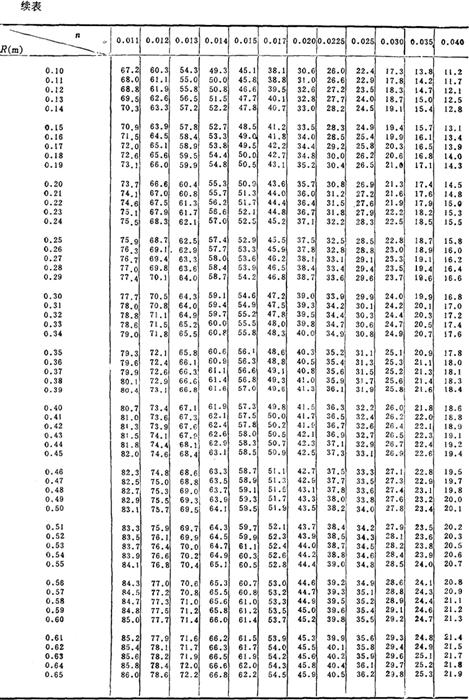
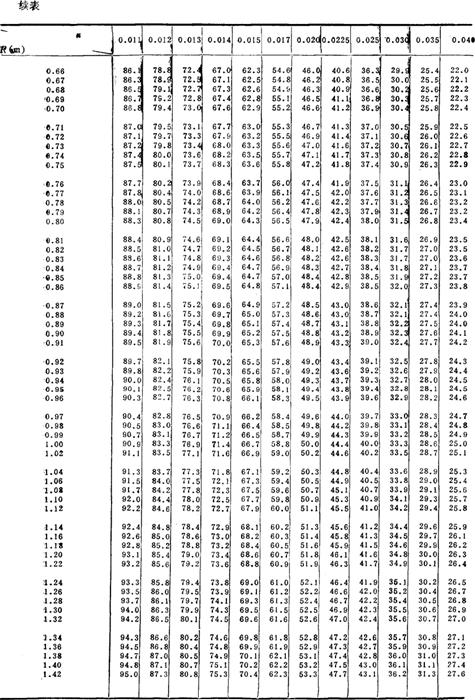
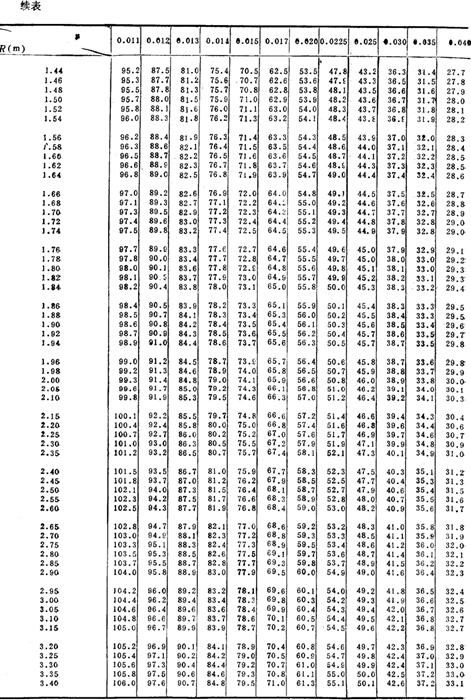
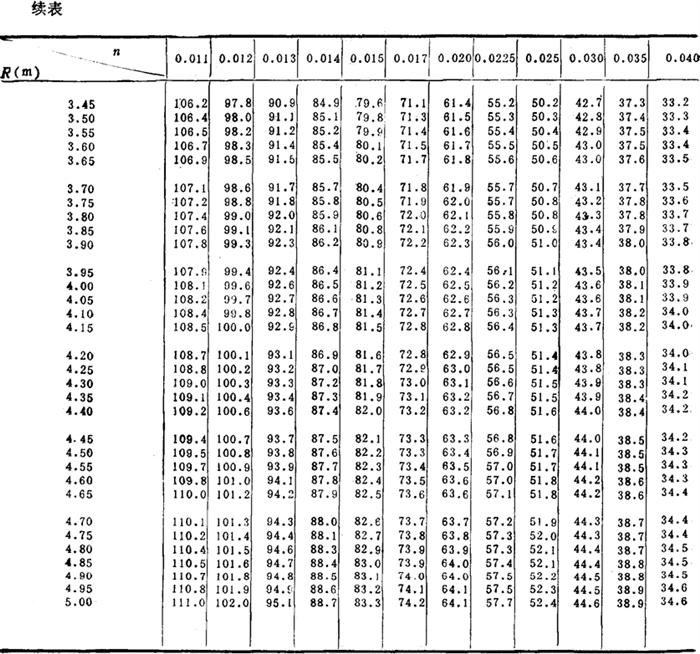
(2)梯形渠道水力最佳断面 指断面面积一定而通过流量最大的断面。梯形渠道水力最佳断面的宽深比β条件为

式中 b0——渠底宽度(m)
h0——渠道水力最佳断面水深(m)
m——边坡系数
依边坡系数m=ctgα而变化的β值,见表2-7-5。
表2-7-5 梯形渠道水力最佳断面宽深比β值

(3)利用图2-7-2计算梯形、矩形断面渠道。
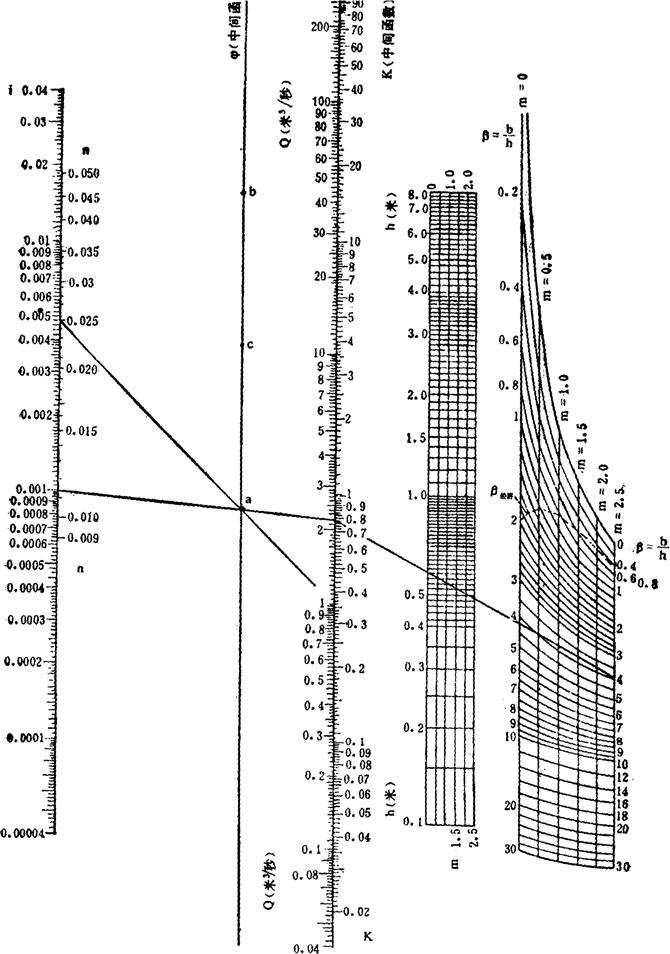
图2-7-2 梯形、矩形、三角形明渠均匀流水力计算共线图
几种图解步骤
1.β-h-K-i-φ-n-Q
2.β-h-K╲
Q-n-φ/
3.Q-n-φ-i-K-h-β
4.Q-n-φ-i-K-β-h
例题(图解1、3)
1.已知b=2m,h=0.5m,m=2.5,i=0.001,n=0.025,求Q=?
先求β=4。
将m=2.5,β=4的点与m=2.5,h=0.5的点相连延长交K轴得K=0.79;
将K=0.79点与i=0.001点相连交φ轴于a点,再将n=0.025与a点相连交于Q轴,得Q=1.01m3/s。
2.已知Q=66m3/s,n=0.03,m=1.5,i=0.0025,h=2.8m,求b=?
联Q=66m3/s及n=0.03相联交φ轴于b点,再将i=0.0025与b点相联,得K=39;
将K=39与m=1.5时的h=2.8m点相连得m=1.5时的β=2.0,
b=β×h=2.0×2.8=5.6m,
计算指示图
本图系根据1965年第一期《水利水电技术》介绍的方法绘制,流量公式为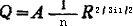
(三)渠道最小边坡
见图2-7-6、2-7-7。
(四)渠堤超高
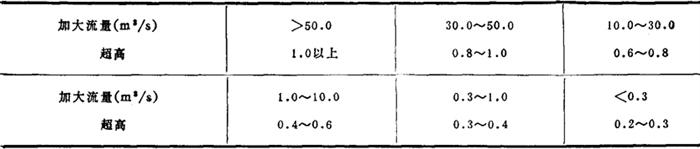
1.输水渠道 一般挖填土渠道的超高,可根据表2-7-8确定。
表2-7-6 挖方渠道最小边坡系数(m)表

表2-7-7 填方渠道最小边坡系数(m)表
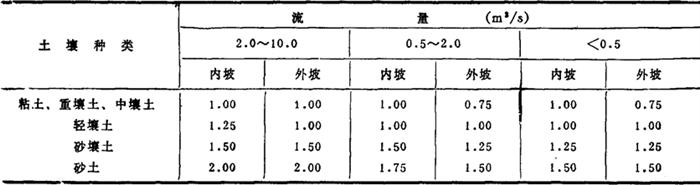
表2-7-8 渠道超高值表
2.衬砌超高 衬砌高度,取决于渠道大小、流量、土壤特性、衬砌材料、渠道用途、渠道所处的位置及渠堤结合道路运用条件等因素,应分别对待,一般输水渠道的衬砌超高采用0.15~0.65。
(五)渠堤宽度
渠岸宽度一般为2~3m且兼作道路时,其宽度应根据公路工程技术标准确定。
挖方渠堤可以比填方堤顶宽度小,但必须满足维修管理的要求。
输水渠道只满足管理运用要求时,渠岸宽度可按下式估算:
D=h+0.3 (2-7-6)
式中 D——渠岸宽度(m)
h——渠道加大流量的水深(m)
- 泥软是什么意思
- 泥轼是什么意思
- 泥辙是什么意思
- 泥途是什么意思
- 泥道是什么意思
- 泥道人是什么意思
- 泥郣头是什么意思
- 泥都都儿是什么意思
- 泥酒是什么意思
- 泥酒情怀似絮,焚香心事如烟。是什么意思
- 泥醉是什么意思
- 泥里倒, 泥里起。是什么意思
- 泥里去是什么意思
- 泥里咕叽是什么意思
- 泥里垢子是什么意思
- 泥里来水里去是什么意思
- 泥里滚水里爬是什么意思
- 泥里狗子是什么意思
- 泥里钻是什么意思
- 泥金是什么意思
- 泥金书是什么意思
- 泥金事是什么意思
- 泥金佳报是什么意思
- 泥金帖是什么意思
- 泥金帖子是什么意思
- 泥金折是什么意思
- 泥金眉子是什么意思
- 泥金膏是什么意思
- 泥金银印花纱是什么意思
- 泥錢是什么意思
- 泥钱是什么意思
- 泥钵擦是什么意思
- 泥铲铲是什么意思
- 泥银是什么意思
- 泥锔锔儿是什么意思
- 泥锹是什么意思
- 泥锹板是什么意思
- 泥镘是什么意思
- 泥阳是什么意思
- 泥阳县是什么意思
- 泥阳川是什么意思
- 泥阳紫荆是什么意思
- 泥阳镇是什么意思
- 泥阳驿是什么意思
- 泥陷是什么意思
- 泥陽是什么意思
- 泥障子是什么意思
- 泥雕是什么意思
- 泥雕木塑是什么意思
- 泥雨是什么意思
- 泥雨城东路,夏槐作云屯。是什么意思
- 泥雪堂是什么意思
- 泥霉是什么意思
- 泥青是什么意思
- 泥靡是什么意思
- 泥鞋是什么意思
- 泥鞋窄袜是什么意思
- 泥頭是什么意思
- 泥頭酒是什么意思
- 泥饭碗是什么意思