标准正交基、正交阵

---

标准正交基 设α₁，α₂，…，α_n∈Rⁿ，且满足

则称｛α₁，α₂，…，α_n｝是Rⁿ的一组标准正交基．

两两正交的非零向量正交必线性无关 Rⁿ中两两正交且不含零向量的向量组α₁，α₂，…，α_n是线性无关的(反之不成立)．

施密特(Schmidt)正交化方法

(1)设α₁，α₂，…，α_s线性无关，若取

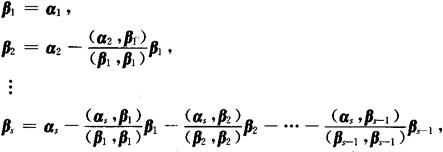
则β₁，β₂，…，β_s是两两正交的非零向量组，将β₁，β₂，…，β_s单位化，即令

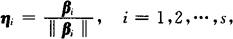
则向量组η₁，η₂，…，η_s是标准正交向量组，上述过程称为施密特正交化方法．

(2)若α₁，α₂，…，α_n是Rⁿ的一组基，按施密特正交化方法得到的两两正交的单位向量组｛η₁，η₂，…，η_n｝，即是Rⁿ的一组标准正交基．

正交矩阵 实数域上的方阵A，若满足

AA^T=E，

则称A为正交矩阵．

A是正交矩阵的充分必要条件 A是正交矩阵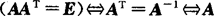的列(行)向量组为Rⁿ的一组标准正交基，即设A=(α₁，α₂，…，α_n)，则有

正交矩阵的性质

(1)E是正交矩阵．

(2)A，B是正交矩阵，则AB也是正交矩阵．

(3)A是正交矩阵，则A^－1(即A^T)也是正交矩阵．

(4)A是正交矩阵，则|A|=1或－1．

(5)A是正交矩阵，则有(α，β)=(Aα，Aβ)，即在正交变换下，向量的内积保持不变，从而保持向量的长度及向量间的夹角不变．