微分方程的基本概念

---

微分方程的定义 凡含有自变量、未知函数以及未知函数的导数或微分的方程称为微分方程．未知函数为一元的叫常微分方程．未知函数为二元或以上的叫偏微分方程．

微分方程的阶、解

(1)微分方程中未知函数的最高阶导数的阶数，叫微分方程的阶．n阶微分方程的一般形式为

F(x，y，y′，…，y⁽ⁿ⁾)=0．

(2)代入微分方程中使之恒等的函数，叫做微分方程的解．

如果微分方程的解中含有任意常数，且任意常数的个数与微分方程的阶数相同，这样的解称为微分方程的通解(这里的任意常数是相互独立的)．不含有任意常数的解称为特解．

微分方程的初始条件 用来确定通解中的任意常数的特定条件，叫初始条件．

一阶微分方程的初始条件是y(x₀)=y₀．

二阶微分方程的初始条件是y(x₀)=y₀，．

n阶微分方程的初始条件是

y(x₀)=y₀，y′(x₀)=y′₀，…，．

初值问题的提法 一阶微分方程的初值问题是指

二阶微分方程的初值问题是指

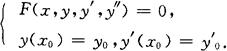
n阶微分方程的初值问题是指

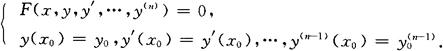
积分曲线 特解y=φ(x)的几何图形是一条平面曲线，叫积分曲线．

通解表示一族曲线，叫做积分曲线族．