实对称矩阵的对角化

---

复矩阵，复向量 元素是复数的矩阵和向量称为复矩阵和复向量

共轭矩阵 设a_ij为复数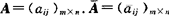．，其中是a_ij的共轭复数，则称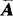是A的共轭矩阵．

共轭向量 设a₁是复数α=(a₁，a₂，…，a_n)^T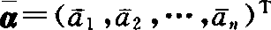，，其中是a_i的共轭复数，则是α的共轭向量．

共轭矩阵，共轭向量的运算性质

(8)当ξ=(a₁，a₂，…，a_n)^T是实向量时，．等号成立当且仅当a_i=0(i=1，2，…，n)

当ξ是n维复向量时，应是

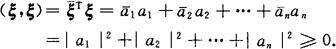
等号成立，当且仅当a_i=0，i=1，2，…，n．

实对称矩阵的对角化

定理1 实对称矩阵A(满足)的特征值都是实数．

定理2 实对称矩阵A的属于不同特征值的特征向量相互正交．

定理3 实对称矩阵A必相似于对角阵．即必存在可逆矩阵P，使得

P^－1AP=A，

且存在正交矩阵Q，使得

Q^－1AQ=Q^TAQ=A，

即A既相似又合同于对角阵．