两个重要的二维分布

---

二维均匀分布

1．密度函数

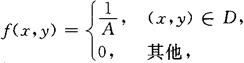
其中A为平面闭域D的面积．

2．性质

(1)若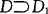，A₁为D₁的面积，则

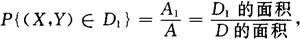
称二维均匀分布满足几何概率．

(2)在正矩形(矩形边与坐标轴平行)上，二维均匀分布的边缘分布是均匀分布，并且X与Y相互独立．

二维正态分布

1．定义，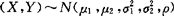

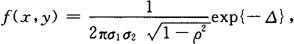
其中

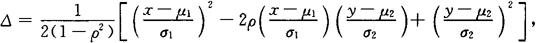
则称(X，Y)服从二维正态分布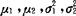．，ρ为参数，且|ρ|＜1．

2．性质

(1)二维正态分布的边缘分布为正态分布，且都与ρ无关．，；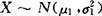

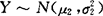(2)二维正态分布中，X，Y相互独立的充分必要条件是ρ=0；

(3)若X，Y独立，μ₁=μ₂=0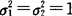，，此时密度函数为

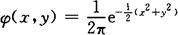
并称为标准正态分布，记为(X，Y)～N(0，0，1，1，0)．