驻相法

---

阶的估计的重要方法。

主要是对积分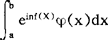进行阶的估计，其中f(x)与φ(x)都是实函数。若将被积函数看作一个向量，则它的相角应该是nf(x)，当f(x)的数值不稳定，即其变化较大时，由于e^inf(x)的数值在－1与1之间交替变化，这样正值与负值“相互抵消”，使得相应的φ(x)e^inf(x)的数值对整个积分值所起的作用仅处于次要地位，而相应于f(x)变化稳定部分φ(x)e^inf(x)的数值，对整个积分值所起的作用，则起著主要作用，这就是驻相法的基本思想。所谓f(x)变化稳定，自然可用条件f’(x)=0来加以描述，使f’(x)=0的点x₀，称为驻相点。关于这方面的主要结果有：(1)设f(z)与φ(z)在包含〔a，b〕的某个单连通域内解析，而且它们在〔a，b〕上均取实值，f’(z)仅在点x=a为零，则当f”(a)＞0时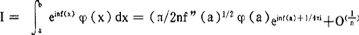，，当f”(a)<0时，I=(－π／2nf”(a)^1／2φ(a)e^{inf(a)－1／4πi}+O^(1／n)；(2)设f(z)与ψ(z)的条件与(1)相同，但f’(z)仅在x=6为零，则当f”(b)＞0时，I=(π／2nf”(b))^1／2ψ(b)e^{inf(b)+1／4πi}+o(1／n)，当f”(b)<0时，I=(－π／2nf”(b)^1／2ψ(b)e^{inf(b)+1／4πi}+0(1／n)；(3)设f(z)与ψ(z)的条件与(1)相同，但f’(a)=0，f”(a)=0，f’”(a)＞0，则I=Г(4／3)(b／nf’”(a))^1／3e^{inf(a)+1／6πi}φ(a)+0(n^－2／3)；(4)设0<λ<1，0<μ<1，φ(x)在〔a，b〕上m次连续可微，f(x)连续可微且有关系式

f’(x)=(x－a)^ρ－1(b－x)^θ－1f₁(x)

其中ρ≥1，θ≥1，f₁(x)在〔a，b〕上正值，而且也是m次连续可微，则

其中A(n)=Am(n)+Rm(n)，B(n)=Bm(n)+Qm(n)，

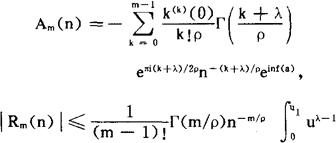
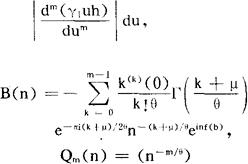
以上结果有许多重要应用，例如，利用(1)及(2)可得，当n→∞时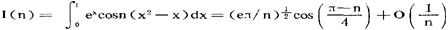，；利用(4)可得，当n→∞时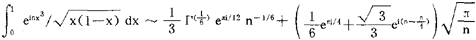，等。