频率特性

---

(1)频率特性定义

若线性定常稳定系统的输入信号为正弦函数，则稳态时其输出也是同频率的正弦函数，但其振幅及相位与输入信号不同，而且是输入信号频率的函数。输入及输出信号分别表示为

x(t)=Asinωt

y(t)=Bsin(ωt+φ)

定义：

·振幅比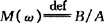，M(ω)随频率的变化关系称为系统的振幅频率特性。简称为幅频特性。

·相位差φ(ω)随频率的变化关系称为系统的相位频率特性。简称为相频特性。

·以M(ω)为模、φ(ω)为幅角所构成的复数M(ω)e^jφ(ω)包括幅频特性和相频特性的性质，称为系统的频率特性。

(2)频率特性与传递函数的关系

M(ω)e^jφ(ω)=G(s)｜_s=jω=G(jω)(5．5－1)

因此，频率特性用G(jω)表示，幅频特性用｜G(jω)｜表示，相频特性用∠G(jω)(或φ(ω))表示。

(3)频域分析法的特点

·该方法是通过分析系统对不同频率谐波输入的稳态响应去识别系统的稳定性、稳态误差和暂态性能。

·频域分析法可用开环系统的频率特性来分析闭环系统的性能，同时又能方便地分析系统某个(或某几个)参数变化对系统性能的影响。

·既然频率特性表现在不同ω的正弦稳态响应上，那么，频率特性就可通过实验获得。

·频域法基本上是一种图解方法。对频域法的作图，目前已有现成的计算机软件做辅助，可用计算机方便地绘制，因此为其应用带来很大方便。